Encodec이란?
by DINHO
논문 리뷰입니다. 저는 계속해서 MusicGen 관련 공부를 해오고 있는데요! 지난 번에 이야기했던 Transformer 에 이어서 MusicGen에서 중요한 개념인 Encodec에 대해 이야기해보겠습니다.
Encodec은 메타에서 진행한 연구로, 2022년 “High Fidelity Neural Audio Compression(Alexandre Défossez, et al.)” 논문에서 처음 소개되었습니다.
Indroduction
논문에서는 스트리밍 오디오 및 비디오가 트래픽의 대부분을 차지하는 최근 경향에 따라 오디오 압축의 필요성을 언급하면서 연구의 목적을 이야기합니다. 압축 과정에는 Bitrate 최소화와 왜곡 최소화를 이뤄내야 하는데, 이 둘은 서로 대립적이라 균형이 필요합니다. 이 논문에서는 기존 신경망 기반 인코더-디코더 메커니즘을 발전시켜 오디오 신호 대상으로 압축 성능 극대화했다고 소개하고 있습니다. Residual Vector Quantization(RVQ)를 사용해 신경망의 출력 잠재 표현을 양자화하여 효율적으로 압축하였습니다. 똣한, 실시간 처리를 위해 단일 cpu 코어에서도 동작 가능하도록 설계되었으며, 다양한 샘플링 속도와 대역폭을 지원합니다.
Related Work
논문에서는 오디오와 신경망 기술, 오디오 코덱 등의 관련 이론들을 이야기하고 있습니다. 간단하게 요약해보았습니다.
-
오디오와 신경망 기술
-
WaveNet: 고품질 오디오 생성을 가능하게 한 최초의 신경망 기반 생성 모델
-
GAN: MelGAN, HiFi-GAN 등은 빠르고 고품질 음성 합성에 성공
-
-
전통적 오디오 코덱
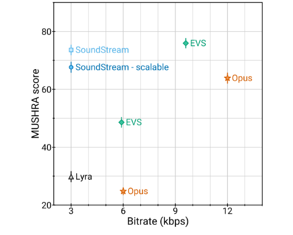
Opus(2012), EVS(2015)등 DSP 기반의 오디오 코덱으로 다양한 Bitrate와 샘플링 속도를 지원하지만 낮은 Bitrate에서는 품질 저하 발생
-
신경망 기반 오디오 코덱
-
LPCNet(2019): 선형 예측 모델 기반으로 데이터를 압축하는 LPC(Linear Predictive Coding) 방법에 WaveRNN을 결합
-
SoundStrem(2021): RVQ를 사용한 신경망 기반 인코더 – 디코더 구조로, Perceptual Loss를 통해 고품질 오디오 복원을 목표로 함
-
-
오디오 이산화 및 변환
- VQ-VAE(2017): 벡터 양자화를 통해 오디오의 이산 표현 학습
이제 모델 구조에 대해서 이야기하겠습니다. 먼저 모델의 개요를 설명 드리고, 논문에서 소개한 소제목대로 설명해보겠습니다.
Model
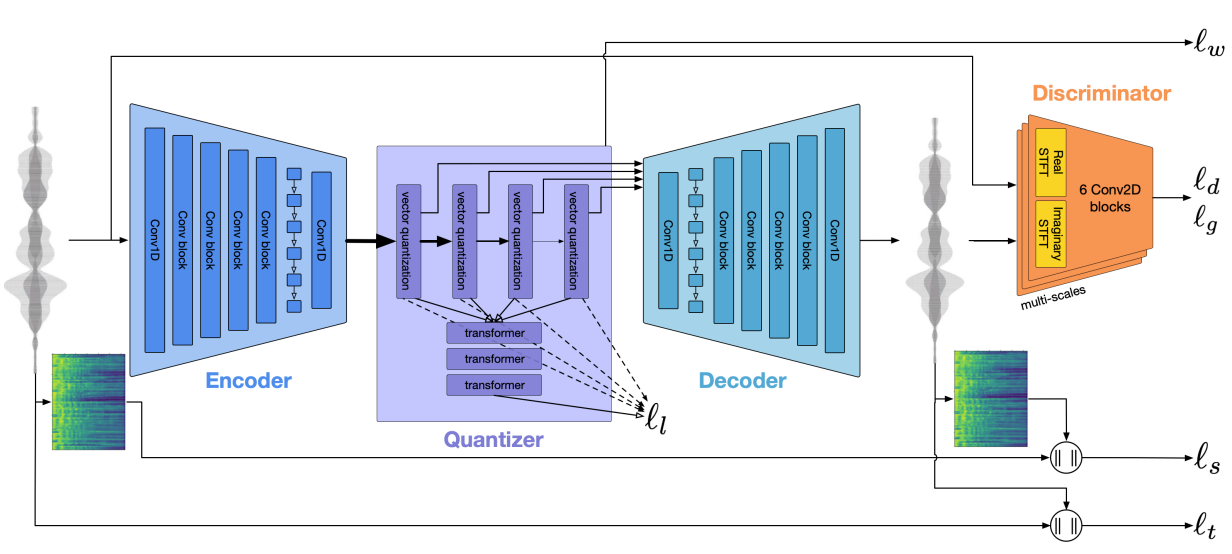
[그림 1] Encodec 구조
전반적인 모델 내용 개요입니다.
Encoder
입력 오디오 𝒙를 잠재 표현 𝒛로 변환합니다. 1D 컨볼루션과 여러 컨볼루션 블록으로 구성되고, 이 구조는 오디오 데이터를 압축 가능한 잠재 공간으로 효과적 매핑을 합니다.
Quantizer
인코더 출력 𝒛를 양자화 하여 압축된 표현 \(z_q\) 으로 변환하고, RVQ를 사용하여 압축 효율을 극대화합니다.
Decoder
압축된 표현 \(z_q\) 을 입력으로 받아 시간 도메인의 오디오 신호 \(\hat{x}\) 를 복원합니다.
이제부터 구체적인 구조를 살펴보겠습니다.
Model - Encoder & Decoder
[그림 1] 에서 보시는 것과 같이 초기 입력은 Conv1D레이어를 거칩니다. 입력 데이터에 대해 32 채널과 커널 크기 k=7을 사용한 1D 컨볼루션을 수행합니다.
이후 4개의 블록으로 구성된 컨볼루션 블록을 지납니다.
잔차 유닛은 k=3의 두 컨볼루션 레이어와 Skip Connection으로 구성되어 있습니다. K=2S, S=(2,4,5,8) 으로 설정한 다운샘플링 레이어를 통해 점진적으로 데이터 크기를 줄입니다. 다운샘플링 이후 채널 수를 두 배로 증가시켜 특징 표현력을 강화합니다.
컨볼루션 블록 출력은 LSTM 레이어를 거쳐 시퀀스 정보를 학습합니다. 이후 마지막으로 커널 크기 k=7을 가진 1D 컨볼루션 레이어를 사용하여 D 채널 잠재 표현을 생성합니다. 활성화 함수로는 ELU 함수를 사용합니다.
디코더는 인코더 구조를 대칭적으로 반전하여 사용합니다. Conv1D 레이어를 통과한 후 LSTM 레이어를 거치고, 컨볼루션 블록에서 S= (8,5,4,2), k=2S 로 설정한 업샘플링 레이어를 통해 점진적으로 압축된 데이터를 해제합니다.
최종 출력은 모노 또는 스테레오 오디오 신호를 생성합니다. (여기서는 압축된 오디오를 복원한 거니까 복원이라는 표현이 맞을수도 있겠습니다.)
Model - None-Streamable
모델에서는 스트리밍 가능한 경우와 아닌 경우를 나눠서 모델의 사용 및 설정을 설명합니다.
먼저 스틀리밍을 사용하지 않는 경우에는 고품질 복원 및 효율적인 처리가 가능합니다. K-S 만큼 입력의 시작과 끝에 동일한 패딩을 추가하여 컨볼루션 경계 문제를 해결하고 입력과 출력 데이터 크기를 유지합니다. 또한, 입력 신호를 1초 단위로 분할하고 각 조각에 10ms 오버랩을 적용하여 클릭 노이즈를 방지합니다. 이때 Layer Normalization을 사용하여 신호를 정규화합니다.
Model - Streamable
스트리밍의 경우에는 실시간 처리와 낮은 지연을 목표로 합니다. 모든 패딩을 입력의 시작 부분에만 적용합니다. 이는 신호가 프레임 단위로 실시간 처리되는데, 각 프레임이 독립적으로 처리되면서 출력이 바로 생성될 수 있기 때문입니다. 한 프레임(S 샘플)을 처리한 뒤 S 샘플을 출력하고, 입력 신호가 도착하면 남은 데이터를 사용하여 프레임을 연결합니다. Weight Normalization을 사용하여 신호를 정규화합니다. (Layer Normalization은 시간 축 통계를 기반으로 하기 때문에 스트리밍 환경에 적합하지 않음)
Model - Residual Vector Quantization
먼저 Vector Quantization(VQ)는 구글에서 구글에서 개발한 방식으로, 입력 벡터를 코드북의 가장 가까운 항목으로 투영하는 방식입니다. 연속적인 데이터를 이산 데이터로 변환합니다. RVQ는 메타에서 개발한 방식으로, VQ에 잔차 학습을 추가한 방식입니다. RVQ는 인코더의 잠재표현을 이산 토큰 시퀀스로 변환하기 위해 사용됩니다.
첫 코드북을 사용해 벡터를 양자화 한 후, 원본 벡터와 양자화 벡터 간 차이(잔차 값)를 계산합니다. 계산된 잔차값을 두 번째 코드북으로 다시 양자회, 이 과정을 반복해 잔차값을 줄이고 양자화 과정의 정확도를 높입니다.
각 단계에서 잔차값을 점진적으로 줄이기 때문에 압축 효율이 높고 복원 품질이 향상됩니다.
이때 잔차 단계를 가변적으로 선택하여 다양한 대역폭을 지원합니다. \(N_{q}\) (코드북 개수)를 4의 배수로 설정하여 1.5, 3, 6, 12, 24 kbps 대역폭을 학습합니다.
24kHz모델은 최대 32개의 코드북과 각 코드북 항목 수는 1024개(10bits) 입니다. 예를 들어 32개의 코드북을 사용하면 \(32 \times 10 = 320 bps\) 대역폭이 됩니다. 24kHz 오디오는 중간 품질의 오디오를 목표로 하며, 상대적으로 더 많은 코드북을 사용하여 세부적인 정보를 더 풍부하게 압축할 수 있습니다.
48kHz모델은 최대 16개의 코드북을 사용합니다. 마찬가지로 각 코드북 항목수는 10bits입니다. 48kHz 오디오는 높은 샘플링 레이트로 더 높은 품질을 제공하고, 상대적으로 더 적은 코드북으로도 충분히 높은 품질을 유지하는 것으로 보입니다. 16개의 코드북은 대역폭을 줄이면서도 48kHz 신호의 세부적은 특성을 표현합니다.
Encodec 모델에서 RVQ는 디코더로 전달되기 전 이산 표현을 다시 벡터 표현을 복원합니다. 선택된 코드북 항목을 모두 합산하여 벡터로 변환합니다.
Model - Language Modeling and Entropy Coding
여기서 말하는 언어 모델은 트랜스포머를 이야기합니다. 트랜스포머와 Entropy Coding을 사용하여 Encodec의 데이터 압축 성능을 극대화 하는 방법을 이야기합니다. 다만 이 방법은 필수는 아닙니다.
압축된 데이터를 더욱 효율적으로 표현하혀, 실시간 처리와 고속 복원을 지원한다고 이야기합니다.
트랜스포머를 통해 코드북의 시간 의존성을 학습하여 이산 표현의 효율성을 극대화합니다. 또한 입력 데이터의 시퀀스를 처리하여 각 코드북의 로그 확률 분호를 예측합니다.
Entropy Coding은 모델의 확률 분포를 기반으로 산술 코딩(Arithmetic)을 수행하여 데이터 압축률을 높입니다.
Model - Training objective
이제 loss에 대해서 이야기해보겠습니다. 손실의 종류가 많지만 어렵지 않습니다!!
Reconstruction Loss
이 loss는 시간 도메인과 주파수 도메인에서 계산되는 loss입니다. 주파수 도메인 loss는 멜-스펙트로그램을 기반으로 합니다.
\[\ell_t(x, \hat{x}) = \|x - \hat{x}\|_1\] \[\ell_f(x, \hat{x}) = \frac{1}{|\alpha| \cdot |s|} \sum_{\alpha_i \in \alpha} \sum_{i \in e} \Big( \|S_i(x) - S_i(\hat{x})\|_1 + \alpha_i \|S_i(x) - S_i(\hat{x})\|_2 \Big)\]Discriminative Loss
이번엔 Discriminative Loss 에 대해 이야기해보겠습니다. 아래 그림은 Encodec의 판별기입니다.
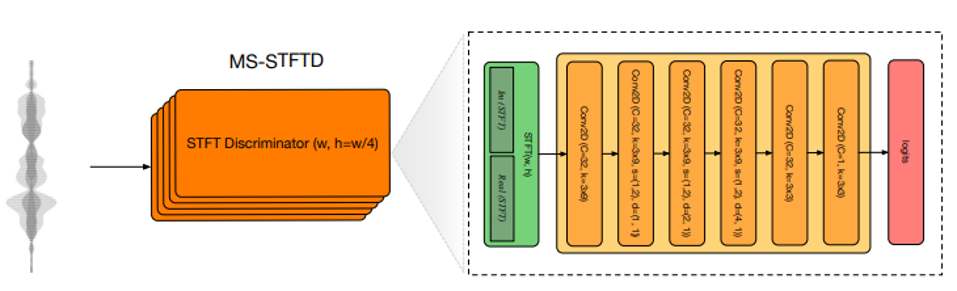
[그림 2] Discriminator 구조
GAN과 동일한 방법으로 판별기를 통해 학습을 합니다. 여기서 생성기는 Encodec이 생성한 신호입니다.
-
Discriminator loss: 힌지 손실(Hinge Loss)를 사용하여 학습하고, 판별기가 Decoder를 지나치게 압도하지 않도록 특정 확률로만 가중치 업데이트
-
Generator loss: 힌지 손실을 사용하여 학습하고, 판별기가 생성된 신호를 진짜로 판단하도록 학습
-
Feature Matching Loss – 판별기의 중간 Feature Maps를 사용하여 생성 신호와 원본 신호 간 차이를 최소화하여 지각적(Perceptual)으로 유사한 오디오를 생성하기 위함임
이 때 \(\mathcal{L}_{\text{feat}}\) 는 Generator의 학습에만 사용됩니다. Generator와 Discriminator 간의 학습 균형을 유지하는 데 기여합니다.
VQ commitment loss
이 loss는 인코더 출력 \(z_{c}\) 와 양자화된 값 \(q_{c}(z_{c})\) 간의 차이를 최소화 하는 데 사용되며, 양자화 과정에서 입력 벡터가 코드북 항목에 잘 매핑되도록 유도합니다. \(q_{c}(z_{c})\) 는 역전파에 포함되지 않아서 gradient 계산이 없습니다.
\[\ell_w = \sum_{c=1}^C \|z_c - q_c(z_c)\|_2^2\]최종 Generator loss는 아래와 같습니다.
\[L_G = \lambda_t \cdot \ell_t(x, \hat{x}) + \lambda_f \cdot \ell_f(x, \hat{x}) + \lambda_g \cdot \ell_g(\hat{x}) + \lambda_{\text{feat}} \cdot \ell_{\text{feat}}(x, \hat{x}) + \lambda_w \cdot \ell_w(w)\]Balencer
각 손실 항목의 gradient 크기가 서로 다를 경우 특정 손실 항목이 학습에 과도한 영향을 미칠 수 있습니다. 따라서 논문에서는 Balencer를 소개합니다. Balencer를 통해 손실 가중치가 손실 크기에 독립적인 기여도로 해석될 수 있습니다. 손실 크기가 서로 달라도 그래디언트의 크기를 보정하여 모든 손실 항목이 균등한 영향을 미칠 수 있도록 조정한다는 뜻입니다.
\[\tilde{g}_i = R \cdot \frac{\lambda_i}{\sum_j \lambda_j} \cdot \frac{g_i}{\langle \|g_i\|_2 \rangle^\beta}\]여기까지 오늘의 포스팅을 마치겠습니다. 논문의 실험 및 결과 부분은 표가 워낙 많아서 생략하도록 하겠습니다. 결론적으로는 Encodec의 효율성과 타당성을 입증하고 있습니다.
Follow my github
