스펙트로그램 & 멜-스펙트로그램 with Python
by DINHO
오늘은 스펙트로그램과 멜-스펙트로그램을 Python에서 다루어보도록 하겠습니다. 설 연휴가 끝나고 오랜만에 게시글을 올리는 만큼 무겁지 않은 주제로 가져와봤습니다😃😃
지난번 FFT with Python 에서 같이 FFT를 적용하고 시간 도메인과 주파수 도메인에서 스펙트럼을 확인해봤었죠?? 이번엔 스펙트럼과 함께 스펙트로그램, 멜-스펙트로그램을 한 눈에 볼 수 있는 Python 코드를 실습해보겠습니다.
먼저 멜-스펙트로그램을 보기 위해서는 librosa 라이브러리를 다운 받아야 합니다. 아래의 커맨드를 터미널에 입력해서 쉽게 다운 받을 수 있습니다.
pip install librosa
지난번 코드에서는 fft, ifft를 적용하고 필터도 적용해서 총 4개의 스펙트럼을 보았는데요. 이번에는 원 신호의 스펙트럼만을 갖고 비교하겠습니다. (지난번처럼 모든 과정에 스펙트로그램과 멜-스펙트로그램을 적용하면 코드가 너무 길어지더라고요… 아래 코드만 공부해도 충분히 어느 상황이든 적용할 수 있을 겁니다😉😉) 전체 코드는 아래와 같습니다. 주요 부분에 대해 설명해드리겠습니다.
import numpy as np
import matplotlib.pylab as plt
import matplotlib.gridspec as gridspec
import pandas as pd
from scipy.io import wavfile
from scipy.signal import spectrogram
import librosa
import librosa.display
from scipy.fft import fft, ifft
from pydub import AudioSegment
# wav file 로딩
audio = AudioSegment.from_file(r"C:\Users\taeso\Desktop\testfft.wav")
# wav 파일 로딩
fs, data = wavfile.read("C:/Users/taeso/Desktop/testfft.wav")
# 데이터를 Float 타입으로 변환
data_float = data.astype(np.float64)
# 데이터의 최대 절대값 찾기
max_val = np.max(np.abs(data_float))
# 신호를 최대 절대값으로 나누어 정규화
norm_data = data_float / max_val
# 시간 축을 생성
time = np.arange(0, len(data)) / fs
# 전체 플롯을 위한 Figure 생성
fig = plt.figure(figsize=(12, 10))
gs = gridspec.GridSpec(3, 1, height_ratios=[1, 1, 1]) # 3개의 행과 1개의 열
# 첫 번째 서브플롯: 시간 도메인 신호
ax1 = fig.add_subplot(gs[0])
ax1.plot(time, norm_data)
ax1.set_title('Normalized Signal in Time Domain')
ax1.set_xlabel('Time [s]')
ax1.set_ylabel('Amplitude')
# 두 번째 서브플롯: 스펙트로그램
ax2 = fig.add_subplot(gs[1])
frequencies, times, Sxx = spectrogram(data, fs, nperseg=1024)
img = ax2.pcolormesh(times, frequencies, 10 * np.log10(Sxx), shading='gouraud')
ax2.set_ylabel('Frequency [Hz]')
ax2.set_xlabel('Time [sec]')
ax2.set_title('Spectrogram')
fig.colorbar(img, ax=ax2, format='%+2.0f dB')
# 세 번째 서브플롯: 멜스펙트로그램
ax3 = fig.add_subplot(gs[2])
S = librosa.feature.melspectrogram(y=norm_data, sr=fs, n_mels=128, fmax=fs/2)
S_DB = librosa.power_to_db(S, ref=np.max)
img = librosa.display.specshow(S_DB, sr=fs, hop_length=512, x_axis='time', y_axis='mel', ax=ax3, fmax=fs/2)
ax3.set_title('Mel Spectrogram')
fig.colorbar(img, ax=ax3, format='%+2.0f dB')
# 첫 번째 서브플롯의 위치와 크기 조정
# 첫 번째 서브플롯을 두 번째 서브플롯과 동일한 너비로 만들기 위해
# ax2.get_position()을 호출하여 두 번째 서브플롯의 위치 정보를 얻습니다.
pos_ax2 = ax2.get_position()
ax1.set_position([pos_ax2.x0, pos_ax2.y0 + pos_ax2.height + 0.1, pos_ax2.width, pos_ax2.height])
# ax3 (세 번째 서브플롯)의 위치를 조정합니다. 이는 ax2와 동일한 높이에서, 하지만 아래에 위치하도록 조정합니다.
ax3.set_position([pos_ax2.x0, pos_ax2.y0 - pos_ax2.height - 0.1, pos_ax2.width, pos_ax2.height])
"""
이런 크기 조정 과정 없이 plt.tight_layout()을 이용하여 자동으로 크기 조절 후 출력할 수 있습니다.
하지만 그렇게 되면 기존 스펙트럼과 (멜)스펙트로그램 plot의 너비가 안 맞더라고요. 그래서 따로 계산해서 크기를 조정해주었습니다.
"""
plt.show()
주요 코드에 대해서 설명하겠습니다.
스펙트로그램
frequencies, times, Sxx = spectrogram(data, fs, nperseg=1024)
이 부분에서는 스펙트로그램에 대한 계산이 들어가 있습니다.
- data: 분석할 오디오 신호 데이터입니다. 이는 일반적으로 NumPy 배열로 표현됩니다.
- fs: 신호의 샘플링 레이트를 나타냅니다. 샘플링 레이트는 초당 샘플 수를 의미하며, 신호의 시간적 해상도를 결정합니다. 일반적으로 오디오는 44.1kHz의 샘플링 레이트를 가지고 있습니다.
- nperseg: 각 세그먼트의 샘플 수를 나타냅니다. 이 값은 주파수 해상도와 시간 해상도 사이의 균형을 결정합니다. nperseg가 크면 주파수 해상도는 높아지지만, 시간 해상도는 낮아집니다.
spectrogram 함수는 주어진 신호에 대해 Short-Time Fourier Transform (STFT)을 계산하여, 시간-주파수 영역에서의 신호의 변화를 나타내는 스펙트로그램을 생성합니다. 이 함수는 주파수 배열(frequencies), 시간 배열(times), 그리고 각 시간 및 주파수 점에서의 스펙트럼의 진폭을 나타내는 Sxx 배열을 반환합니다.
img = ax2.pcolormesh(times, frequencies, 10 * np.log10(Sxx), shading='gouraud')
이 부분에서는 스펙트로그램에 대한 시각화 과정을 나타냅니다.
- times: 스펙트로그램의 각 열이 대응하는 시간 배열입니다.
- frequencies: 스펙트로그램의 각 행이 대응하는 주파수 배열입니다.
- 10 * np.log10(Sxx): Sxx 배열의 값들을 데시벨 단위로 변환합니다
- shading=’gouraud’: 이 옵션은 색상 사이의 전환을 부드럽게 하는 보간 방법을 지정합니다. ‘gouraud’ 보간은 인접한 색상 사이에서 부드러운 그라데이션을 생성하여, 시각적으로 매끄러운 이미지를 만듭니다.
멜-스펙트로그램
S = librosa.feature.melspectrogram(y=norm_data, sr=fs, n_mels=128, fmax=fs/2)
이 부분에서는 오디오 신호를 멜 스케일로 변환된 스펙트로그램으로 변환하는 과정, 즉, 멜-스펙트로그램을 생성하는 과정입니다.
- y=norm_data: 이는 분석할 오디오 데이터입니다. 여기서는 정규화된 데이터를 사용합니다.
- sr=fs: sr은 오디오 데이터의 샘플링 레이트를 나타냅니다. fs는 파일에서 읽은 샘플링 레이트입니다.
- n_mels=128: 멜 스펙트로그램을 계산할 때 사용할 멜 필터 뱅크의 수입니다. 이 값이 높을수록 주파수 해상도가 높아집니다.
- fmax=fs/2: 분석할 최대 주파수를 나타냅니다. 일반적으로 Nyquist 이론에 따라 샘플링 레이트의 절반까지가 최대 주파수 범위입니다.
S_DB = librosa.power_to_db(S, ref=np.max)
이 단계는 스펙트로그램의 값들을 데시벨 단위로 변환하여, 시각적으로 더 명확하게 대비를 볼 수 있게 합니다.
- S: 멜 스펙트로그램의 파워 값을 입력으로 합니다.
- ref=np.max: 데시벨 스케일로 변환할 때의 참조 값입니다. 여기서는 S의 최대값을 참조 값으로 사용하여 모든 값이 0 dB 이하가 되도록 합니다.
- S_DB: 데시벨 단위로 변환된 멜 스펙트로그램 데이터입니다.
img = librosa.display.specshow(S_DB, sr=fs, hop_length=512, x_axis='time', y_axis='mel', ax=ax2, fmax=fs/2)
이 단계에서는 멜 스펙트로그램을 시간-멜 스케일에서 시각화하여, 오디오의 시간에 따른 주파수 변화를 쉽게 관찰할 수 있게 해줍니다.
- hop_length=512: STFT(Short-Time Fourier Transform) 계산 시 각 프레임 사이의 샘플 수입니다. 이 값이 크면 시간 해상도는 낮아지고 주파수 해상도는 높아집니다.
- x_axis=’time’, y_axis=’mel’: x축은 시간을, y축은 멜 스케일을 나타냅니다.
- ax=ax2: matplotlib의 축 객체입니다. 이 함수는 지정된 축에 그래프를 그립니다.
- fmax=fs/2: 시각화할 최대 주파수 범위를 지정합니다.
아래는 위 코드를 실행하여 얻은 결과 이미지입니다.
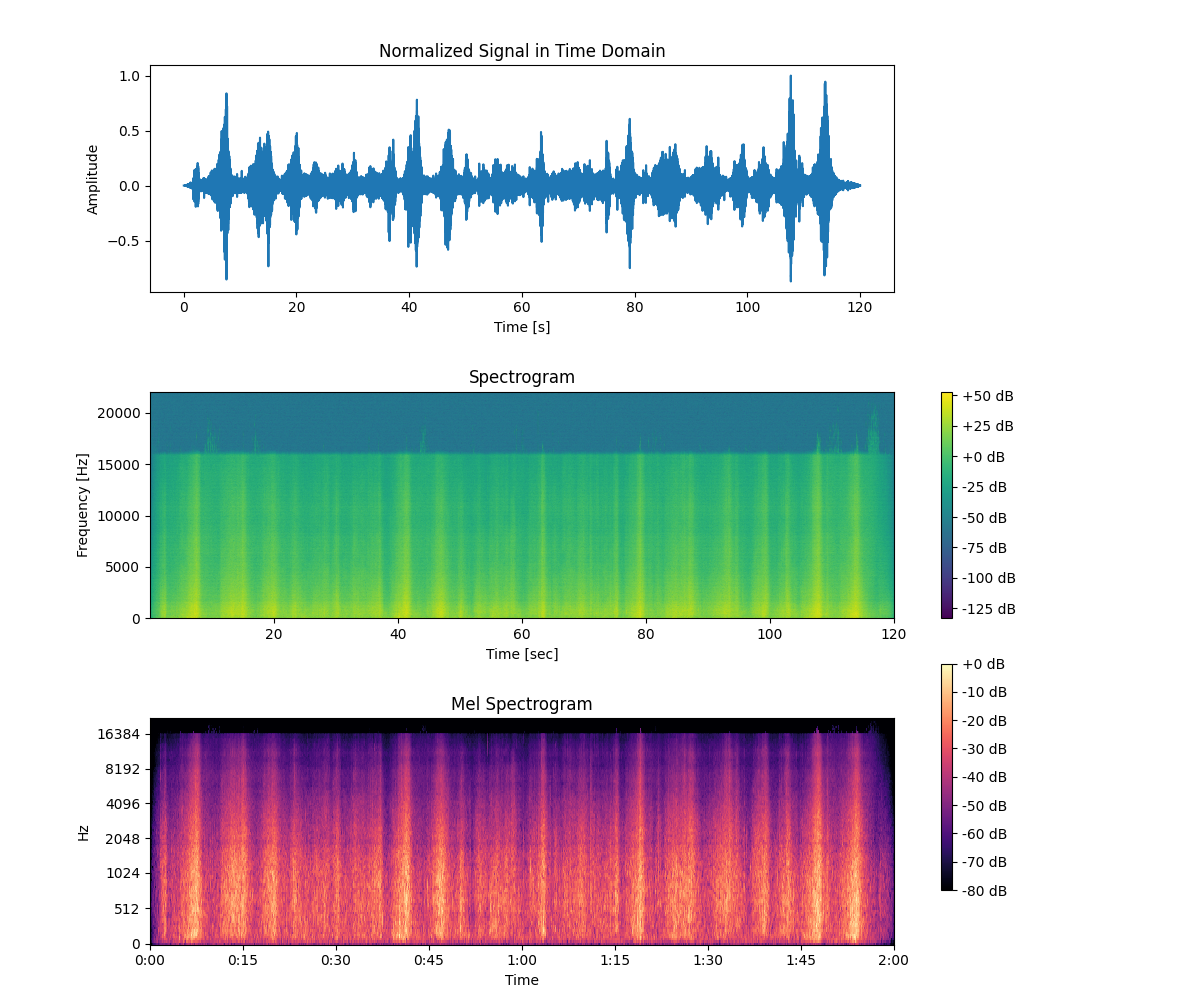
차이가 느껴지시나요? 확실히 범위가 달라졌다는 것을 시각적으로 느낄 수 있습니다!!
제 블로그를 찾아주시는 분들의 대부분이 FFT 같은 신호 처리 관련 코드나 개념의 글들을 많이 보시는 것 같습니다. 열심히 공부해서 올린 논문 리뷰는 아무도 안 본다는 슬픈 이야기가…😂😂
그만큼 이 분야의 기초 지식을 쌓고 계신 분들이 많으시다는 거겠죠!! 저도 아직 부족한 만큼 기초를 계속 반복하고 복습해서 여러분들께 정확하고 자세하게 알려드리겠습니다😊😊
Follow my github
