FFT with Python
by DINHO
오늘은 디지털 신호처리의 기초!! FFT에 대해서 아주 간단하게 언급하고 Python과 함께 직접 적용해보도록 하겠습니다. 이 글은 기본적인 디지털 신호 처리 과정, DFT의 내용을 알고 있다고 생각하고 글을 쓰겠습니다😄 나중에 기회가 된다면 신호 처리 생초보를 위한 디지털 신호 처리 이론도 다루어보도록 하겠습니다😋😋
FFT 기초
FFT(Fast Fourier Transform)는 DFT(Discrete Fourier Transform)를 빠르게 수행하기 위한 알고리즘입니다. DFT는 아래의 식처럼 정의가 가능합니다.

DFT 정의에 따라 계산하면 O(N 2)의 연산이 필요하지만, FFT를 이용하면 O(N log N)의 연산만으로 가능하기 때문에 굉장히 빠른 계산이 가능합니다. 아래 이미지는 빅오 표기법을 눈으로도 이해하기 쉽도록 이미지를 첨부하였습니다.
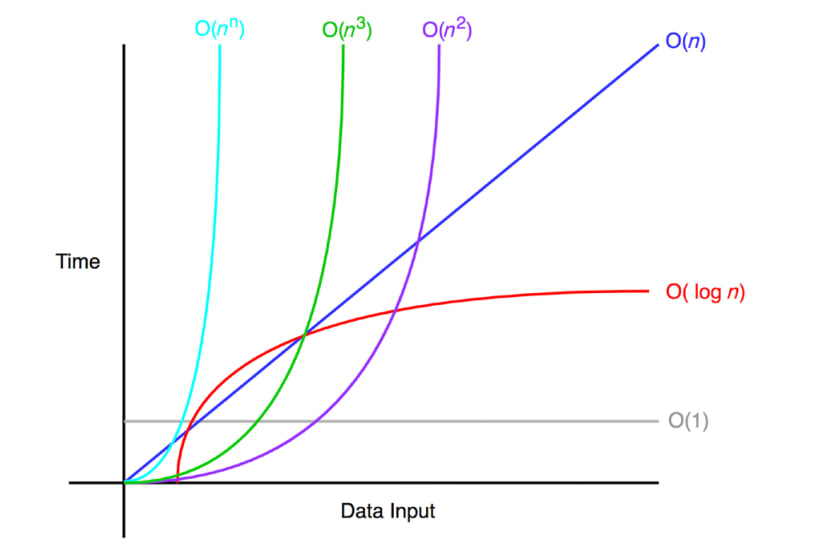
FFT VS DFT
계산 시간에 대해서 코드로 직접 비교해보겠습니다. 아래는 기본 라이브러리를 이용해 DFT를 구현한 C코드의 일부입니다. 제가 전공 과제를 하기 위해 다음과 같이 DFT를 구현했었는데요. 이때 문제가 있었습니다. 바로 DFT를 구현하기 위해 4중 for문을 사용한다는 점인데요. 당시 DFT를 적용한 이미지가 512*512크기의 Lena.raw파일이였는데, dft 돌리는데 진짜 몇 시간이나 걸렸습니다.
근데 이 부분을 FFT로 구현하면 어떻게 될까요??
// Function to compute the 2D DFT
void computeDFT(unsigned char* imageData, double* outputReal, double* outputImag) {
for (int u = 0; u < WIDTH; u++) {
for (int v = 0; v < HEIGHT; v++) {
double sumReal = 0.0;
double sumImag = 0.0;
for (int x = 0; x < WIDTH; x++) {
for (int y = 0; y < HEIGHT; y++) {
int index = y * WIDTH + x;
double angle = 2 * PI * ((u * x / (double)WIDTH) + (v * y / (double)HEIGHT));
sumReal += imageData[index] * cos(angle);
sumImag += -imageData[index] * sin(angle);
}
}
outputReal[u + v * WIDTH] = sumReal;
outputImag[u + v * WIDTH] = sumImag;
}
}
}
위에는 DFT,아래는 FFT를 기본 라이브러리를 이용해서 적은 C코드의 일부입니다. 보시다 시피 4중 for문이 없어지고 2중 for문 많으로 계산할 수 있어서 비교할 수 없을 만큼 빠릅니다.
// 2D FFT implementation
void fft2D(Complex* data, int width, int height) {
// Apply 1D FFT row-wise
for (int y = 0; y < height; y++) {
fft1D(data + y * width, width);
}
// Apply 1D FFT column-wise
Complex* temp = (Complex*)malloc(sizeof(Complex) * width);
for (int x = 0; x < width; x++) {
for (int y = 0; y < height; y++) {
temp[y] = data[y * width + x];
}
fft1D(temp, height);
for (int y = 0; y < height; y++) {
data[y * width + x] = temp[y];
}
}
free(temp);
}
이제 DFT를 안 쓰고 FFT를 쓰는 이유를 아시겠나요?? 그렇다면 본격적으로 Python을 이용해서 FFT를 직접 실습해보도록 하겠습니다. 이번 실습에서는 임의의 mp3파일로 진행하겠습니다. 1D 신호이기 때문에 2D인 이미지보다 직관적으로 와닿으실 겁니다!!
이번 실습 과정은 다음 이미지와 같습니다.
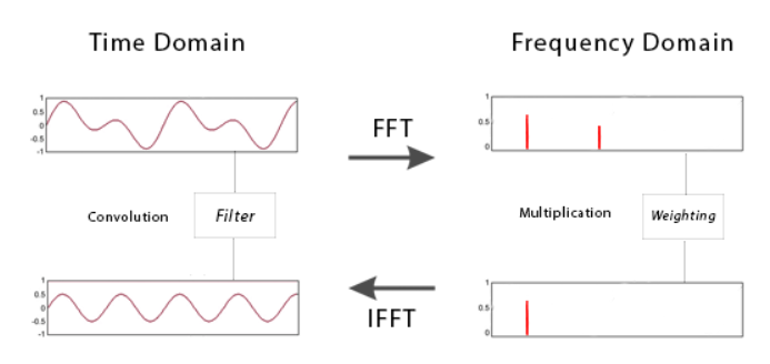
- 먼저 시간 도메인에서 음성 신호의 Amplitude를 확인
- FFT를 적용하여 주파수 도메인에서 Amplitude를 확인
- Band-pass 필터를 적용하여 주파수 도메인에서 Amplitude를 확인
- 필터를 적용한 신호를 시간 도메인에서 Amplitude를 확인
아래는 Python Code입니다. 한 줄 한 줄 따라 써보시면서 전체적인 흐름을 이해하시면 FFT를 쉽게 이해하실 수 있을 겁니다.
import numpy as np
import matplotlib.pylab as plt
import pandas as pd
from scipy.io import wavfile
from scipy.signal import spectrogram
from scipy.fft import fft, ifft
from pydub import AudioSegment
# mp3 file 로딩
audio = AudioSegment.from_file(r"C:\Users\Home\Desktop\testfft.MP3")
# mp3 파일을 모노로 변환하고 wav형식으로 변환
"""
기본적으로 FFT를 하려먼 1차원 음성 신호여야 합니다.
MP3는 대부분 스테레오 타입이 많아서 좌우로 분리된 오디오 채널이 많습니다.
MP3는 압축 포맷이기 때문에 압축되지 않은 오디오 파일 형식인 WAVV파일을 이용해야 합니다.
"""
audio = audio.set_channels(1)
audio.export("C:/Users/Home/Desktop/testfft.wav", format="wav")
# wav 파일 로딩
fs, data = wavfile.read("C:/Users/Home/Desktop/testfft.wav")
# 데이터를 Float 타입으로 변환
data_float = data.astype(np.float64)
# 데이터의 최대 절대값 찾기
max_val = np.max(np.abs(data_float))
# 신호를 최대 절대값으로 나누어 정규화
norm_data = data_float / max_val
# 시간 축을 생성
time = np.arange(0, len(data)) / fs
#정규화된 시간 도메인 신호 그림 생성
plt.figure(figsize=(12, 6))
plt.plot(time, norm_data)
plt.title('Nomalized Signal in Time Domain')
plt.xlabel('Time(seconds)')
plt.ylabel('Amplitude')
plt.show()
# Hamming window 적용
hamming_window = np.hamming(len(norm_data))
windowed_data = norm_data * hamming_window
# fft 수행
fft_data = fft(windowed_data)
# 주파수 도메인 스펙트럼 plot
frequencies = np.linspace(0, fs, len(fft_data))
plt.figure(figsize=(12, 6))
plt.plot(frequencies[:len(frequencies)//2], np.abs(fft_data)[:len(frequencies)//2]) # plot only the positive frequencies
plt.title('Frequency Spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.show()
# 주파수 배열 생성
frequencies = np.linspace(0, fs, len(fft_data)//2)
# 밴드 패스 필터 적용
f_low = 1500
f_high = 6000
band_pass_filter = (frequencies >= f_low) & (frequencies <= f_high)
fft_data_filtered_half = fft_data[:len(fft_data)//2]
fft_data_filtered_half[(frequencies < f_low) | (frequencies > f_high)] = 0
# 대칭성을 유지하면서 전체 FFT 데이터 길이로 필터링된 데이터를 확장
fft_data_filtered = np.concatenate((fft_data_filtered_half, np.conj(fft_data_filtered_half[-2:0:-1])))
# 필터링된 신호를 시간 도메인으로 변환
filtered_data = ifft(fft_data_filtered)
# 실수 부분만 사용하여 시간 도메인 신호 획득
filtered_data_real = np.real(filtered_data)
# 주파수 도메인의 필터링된 신호 그림 생성
plt.figure(figsize=(12, 6))
plt.plot(frequencies[:len(frequencies)//2], np.abs(fft_data)[:len(frequencies)//2])
plt.title('Filtered Frequency Spectrum')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.show()
# 필터링된 신호의 길이에 맞춰 time 배열의 길이 조정
time = time[:len(filtered_data_real)]
#필터링된 신호를 시간 도메인에서 그림 생성
plt.figure(figsize=(12, 6))
plt.plot(time, filtered_data_real)
plt.title('Filtered Signal in Time Domain')
plt.xlabel('Time (seconds)')
plt.ylabel('Amplitude')
plt.show()
# 정규화 해제
filtered_data_unnormalized = filtered_data_real * max_val
# 16비트 정수형으로 변환
filtered_data_int16 = np.int16(filtered_data_unnormalized)
# 필터링된 신호를 WAV 파일로 저장
wavfile.write('C:/Users/Home/Desktop/testfft_filtered.wav', fs, filtered_data_int16)
아래는 결과 이미지 입니다. 필터링도 잘 적용 됐고, 음성 신호의 주파수 특성을 파악할 수 있습니다.

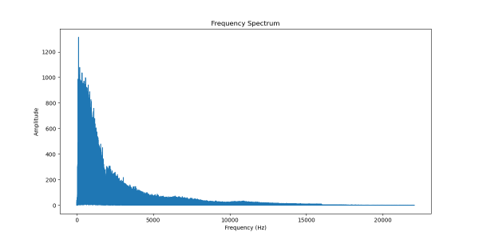
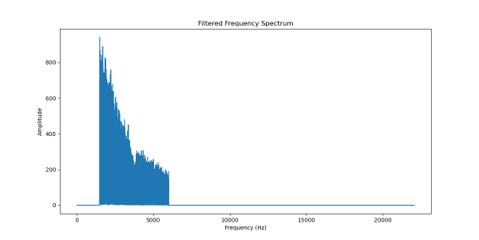

다음에는 위에서 얻은 그래프와 함께 스펙트로그램도 출력시켜보겠습니다. 이번 글은 길지만 그만큼 알찬 내용이라 생각합니다.
도움이 되셨길 바랍니다😁😁
Follow my github
