제가 여름 방학 때 공부하면서 딥러닝에 대한 포스팅을 하기 위해 딥러닝 소개 를 포스팅했었는데요. 그 뒤로 공부만 하고 포스팅을 하지 못 했습니다…😅😥 이모저모 바쁘게 8월을 보내고 바로 학기가 시작하는 바람에 이렇게 되어 버렸네요… 이번 겨울 방학에는 무조건 이 시리즈를 마무리하겠습니다.🤩🤩(☞ﾟヮﾟ)☞(。・∀・)ノ

그럼 지난 포스트에 이어서 딥러닝 소개 2탄 시작하겠습니다.

Building Neural Networks with Perceptrons

지난 포스트에서 신경망들이 어떻게 작동되는지 살펴보겠다고 했는데요!! 먼저 뉴런(퍼셉트론)을 간단하게 표현해보겠습니다.

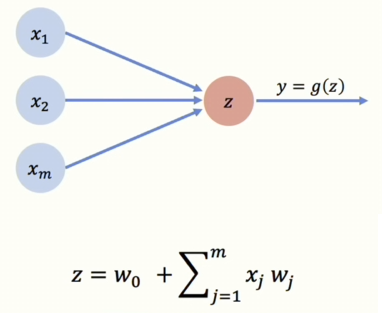
[그림 1] Simplifed Perceptron

이렇게 간단하게 해도 결국 이것만 기억하시면 됩니다. 입력과 가중치를 내적하고 바이어스를 더해서 비선형활성화함수를 통과시킨다!! 간단화한 그림은 출력 y가 g(z)로 간단하게 표현되고 있습니다.

그렇다면 이제 출력이 두 개이면 어떻게 될까요?

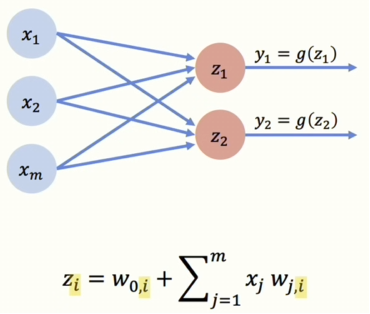
[그림 2] Multi OutPut Perceptron

각 뉴런은 하나의 답을 예측하게 될 겁니다. 이렇게 다중 뉴런에서 가장 중요한 것은 각 뉴런마다 고유한 가중치를 가진다는 것입니다. 이들은 독립적으로 소통하지만 나중에 다른 층이 추가되면 서로 소통할 수 있습니다. 모든 입력이 모든 출력과 densly하게 연결되어 있어서 이러한 레이어들을 Dense layers라고 합니다.

이 과정을 프로그래밍적으로 생각해보겠습니다. 수식들이 어렵지 않았으니 비교적 간단하게 구현되겠죠?

# tensorflow사용 예제
import tensorflow as tf
class MyDenseLayer(tf.keras.layers.Layer):
	def __init__(self, input_dim, output_dim):
		super(MyDenseLayer, self).__init__()

		# Initialize weights and bias
		self.w = self.add_weight([input_dim, output_dim])
		self.b = self.add_weight([1, output_dim])

	#실제로 정보가 레이어를 통해서 어떻게 전달 되는지 보기 위해 호출 함수 생성 
	def call(self, inputs):
		# Forward propagate the inputs
		z = tf.matmul(inputs, self.w) + self.b

		# Feed through a non-linear activation
		output = tf.math.sigmoid(z)

		return output

# pytorch사용 예제
import torch
import torch.nn as nn
class MyDenseLayer(nn.module):
	def __init__(self, input_dim, output_dim):
		super(MyDenseLayer, self).__init__()

		# Initialize weights and bias
		self.w = nn.Parameter(torch.radn(input_dim, output_dim, requires_grad=True))
		self.b = nn.Parameter(torch.radn(1, output_dim, requires_grad=True))

	#실제로 정보가 레이어를 통해서 어떻게 전달 되는지 보기 위해 호출 함수 생성 
	def call(self, inputs):
		# Forward propagate the inputs
		z = tf.matmul(inputs, self.w) + self.b

		# Feed through a non-linear activation
		output = tf.math.sigmoid(z)
		return output

하지만 최근 딥러닝 툴박스와 라이브러리들이 이미 많은 것을 구현해주기 때문에 한 줄로 딸깍 할 수 있습니다.

# tensorflow
import tensorflow as tf

layer = tf.keras.layers.Dense(units=2)

# pytorch
import torch
import torch.nn as nn

layer = nn.Linear(in_features=m,out_features=2)

신경망의 복잡성을 천천히 높여보겠습니다.

여기 Single Layer Neural Network를 보겠습니다.

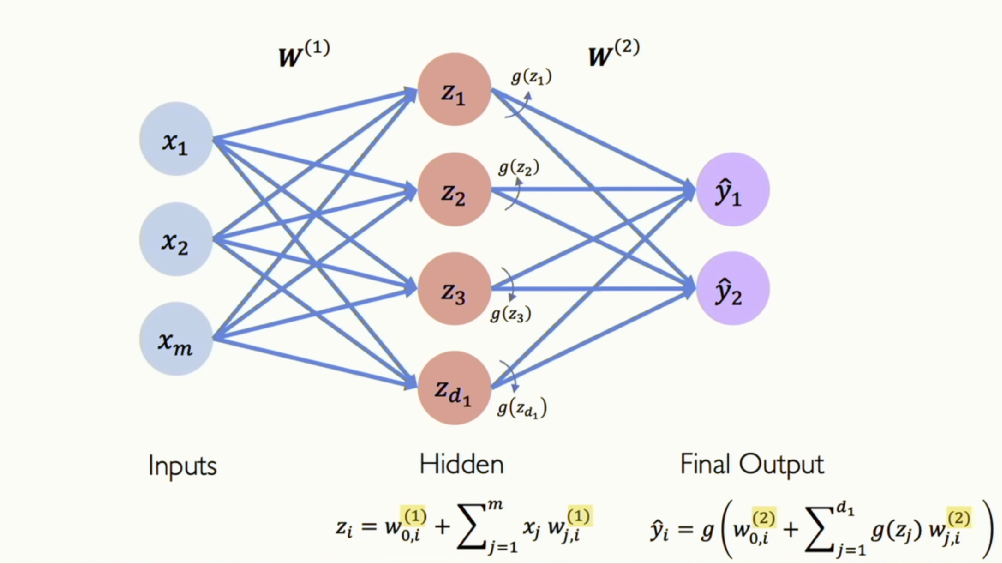
[그림 3] Single Layer Neural Network

가운데에 있는 레이어는 히든 레이어(Hidden Layer)라고 합니다. 직접적으로 관찰하거나 감독할 수 없어서 그렇게 부릅니다. 입력과 출력은 직접 관찰할 수 있지만, 히든레이어는 볼 수 없습니다. 아까 그림과는 다르게, 이제는 입력에서 히든 레이어로, 히든 레이어에서 출력으로 변환하는 함수가 있으니 레이어가 2개인 신경망을 가지게 됐습니다. 즉, 두 개의 가중치 행렬을 가지게 됩니다.

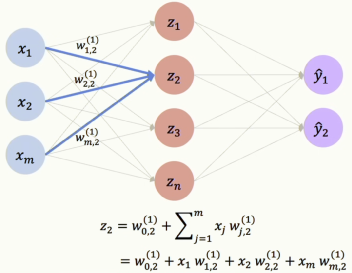
[그림 4] Single Layer Neural Network

히든레이어의 단일 유닛을 한 번 보겠습니다. Z2를 예로 보겠습니다. 이 뉴런의 값을 구하는 것은 계속 이야기 한 것과 동일합니다. 가중치와 입력값의 내적을 구하고, 바이어스를 더한 수 비선형활성화함수를 적용하면 됩니다. Z3, Z4도 마찬가지입니다. 가중치 값만 다를 뿐, 답을 구하는 방법은 같습니다.

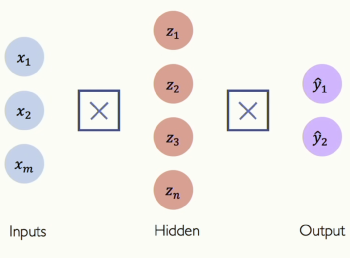
[그림 5] Multi OutPut Perceptron

이제 그림을 좀 단순화 해서 모든 연결 선을 박스 기호로 대체하겠습니다. 이 기호는 Fully Connected Layer를 뜻합니다. 아까 코드를 잠깐 봤으니 이 그림도 간단하게 코드로 구현할 수 있습니다.

# Tensorflow
import tensorflow as tf

model = tf.keras.Sequential([
	tf.keras.layers.Dense(n),
	tf.keras.layers.Dense(2)
])

# Pytorch
from torch import nn

model = nn.Sequential(
	nn.Linear(m,n),
	nn.ReLU(),
	nn.Linear(n,2)
)

이제는 이전과 달리 단순한 신경망이 아니라 더 깊어진 신경망을 보겠습니다.

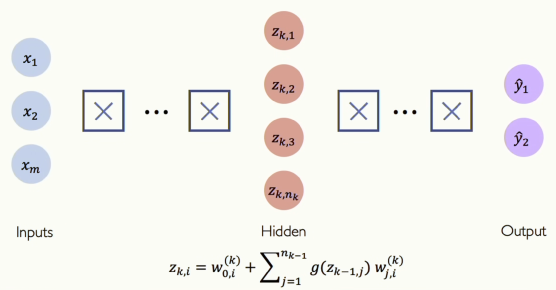
[그림 6] Deep Neural Network

레이어들을 하나씩 쌓아가며 점점 더 계층적인 모델을 만들 수 있습니다. 최종 출력은 신경망을 점점 더 깊게 깊게 통과하면서 계산됩니다.

코드로 구현할 때도 같습니다. 코드 내부에서 층들을 차례로 쌓아가면서 네트워크를 깊게 만들면 됩니다.

이러한 기초 지식들로 신경망을 적용하는 방법에 대해 이야기해보겠습니다.

Applying Neural Network

가장 유명한 예시를 들어보겠습니다.

Will I pass this class?

간단한 두 feature 모델과 함께 시작하겠습니다. \(x_{1}\) 은 강의 출석 수이고 \(x_{2}\) 는 최종 프로젝트에 투자한 히간이라 하겠습니다.

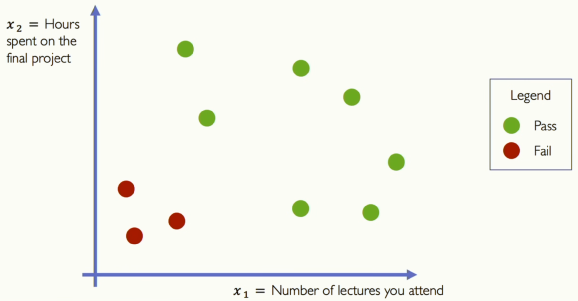
[그림 7] Example Problem: Will I pass this class?

몇 년 간의 수업 관찬을 토대로 위와 같은 데이터가 있다고 합시다. 한 점은 사람을 나타내고 ,색깔은 수업 통과 여부를 나타냅니다.

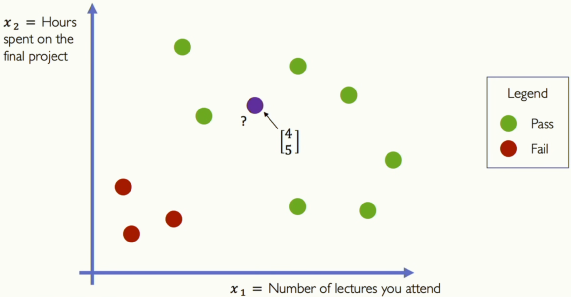
[그림 8] Example Problem: Will I pass this class?

제가 보라색이라고 해보겠습니다. 이 피처 공간에 [4,5] 지점이 있다고 해보겠습니다. 이제 신경망을 구축하고, 이전 수업들의 모든 학생들의 정보를 이용해 신경망이 제가 수업을 통과할 가능성에 대해 예측하는 겁니다.

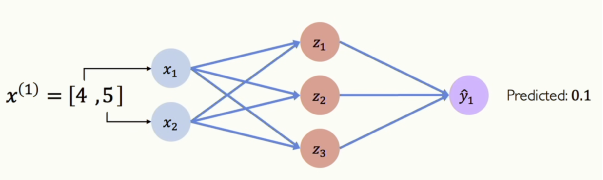
[그림 9] Example Problem: Will I pass this class?

현재 두 개의 입력 값이 있습니다. 이 값들은 단일 히든레이어 신경망에 입력됩니다. 이 때 예측된 확률은 10%라는 것을 알 수 있습니다. 하지만 위에 그림을 봤었을 때 비교하면 타당해 보이나요?? 그렇지 않습니다. 수업 5 번 중 4 번을 참여했고 프로젝트에 5시간을 투자하였으니 실제로는 수업에서 통과할 겁니다. 왜 이런 터무니 없는 예측을 했을까요? 아직 위 그림의 데이터를 보여주지 않았기 때문읍니다. 즉, 신경망 훈련이 안 됐기 때문입니다. 우리는 이 신경망을 훈련시켜야 합니다. 이제 신경망을 훈련시켜보겠습니다.

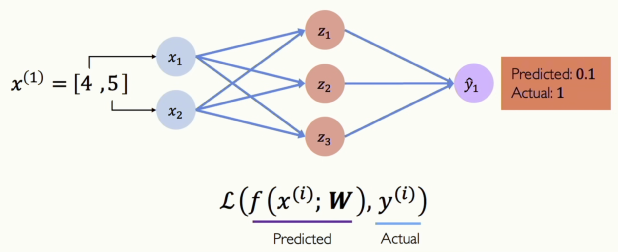
[그림 10] Quantifying Loss

먼저 신경망을 훈련시키려면 신경망이 잘못된 결정을 내릴 때마다 알려줘야 합니다. 우리는 이것을 Loss(손실)라고 합니다. 실제 값과 예측 값의 차이를 계산하고, Loss를 줄이는 방식으로 학습합니다. Loss 함수에는 여러 종류가 있습니다. L1, L2 거리, Cross-Entropy 등등 다양한 Loss 종류들이 있습니다.

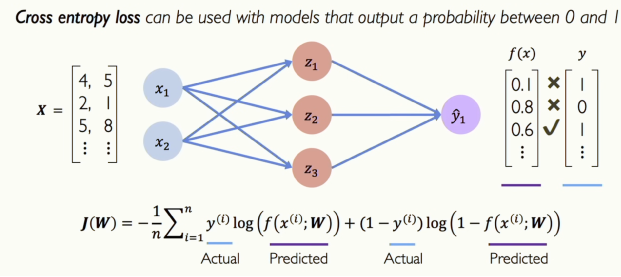
[그림 11] Binary Cross Entropy Loss

한 학생뿐 아니라 여러 학생들의 데이터로 학습을 하고 Loss를 줄이며 신경망은 학습하게 됩니다. 예측과 실제 값이 가까울수록 손실은 작아져야 하고, 모델의 정확도는 높아져야 합니다.

이 신경망에게 정답을 알려주기 위해 그림처럼 Softmax(Softmax Cross-Entropy)를 사용할 수 있습니다. Softmax는 신경망에게 두 확률 분포가 얼마나 떨어져 있는지 알려주는 손실함수입니다. 그래서 출력은 확률 분포가 되고, 신경망이 더 나은 답을 내도록 피드백할 수 있게 됩니다.

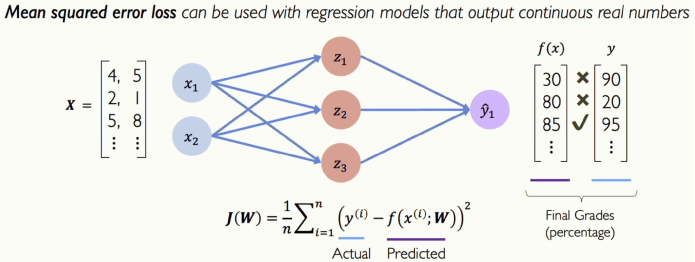
[그림 12] Mean Squared Error Loss

이제 이진 출력을 예측하거나 훈련하는 대신, 임의의 숫자를 예측하고 싶으면 어떡할까요? 그 숫자는 양의 무한대부터 음의 무한대까지 어떤 숫자든 될 수 있습니다. 즉 제가 받을 학점을 예측하고 싶다면 그 학점이 꼭 0에서 1이거나 0에서 100일 필요는 없습니다.

MSE(Mean Squared Error)라는 손실을 사용해서 그 값을 만들 수 있습니다. 이 경우에는 확률분포가 아닌 수업에서 받은 진짜 학점과 예측된 학점 사이의 MSE를 계산 할 수 있겠네요. 부호는 상관 없이, 제곱하여 거리를 계산한 값이 MSE입니다. 결국 신경망은 Loss를 최소화 하여 입력값에 대한 출력을 예측하는 것입니다.

Training Neural Networks

그렇다면 손실 정보와 네트워크 가중치를 찾는 문제를 하나로 합쳐보겠습니다. 우리는 결국 이 방대한 데이터에 대해 평균적으로 문제를 해결할 수 있는 신경망을 찾고 있는 겁니다.

\[W^* = \underset{W}{\arg\min} \frac{1}{n} \sum_{i=1}^n \mathcal{L}(f(x^{(i)}; W), y^{(i)}) W^* = \underset{W}{\arg\min} J(W)\]

즉 우리가 찾는 것은 신경망의 가중치가 무엇인지입니다. 계속 예기한 벡터 W를 찾고 싶습니다. 모든 데이터를 바탕으로 이 벡터 W를 계산할 수 있습니다. 그리고 이 벡터 W는 손실이 어떻게 될지도 결정합니다. 손실은 뭐였죠? 신경망이 예측한 값과 실제 값에서 얼마나 벗어났는지 나타내던 거였습니다.

이 가중치 벡터는 숫자들의 모음이라는 것을 잘 생각해봅시다. 그래서 많은 데이터를 바탕으로 얻은 이 벡터는 무엇일까요? 그것이 신경망을 학습해야 할 문제입니다.

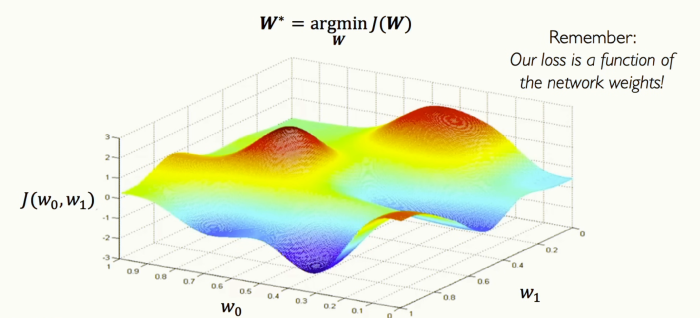
[그림 13] Loss Optimization

이전에 봤던 것처럼 신경망에 가중치가 두 개밖에 없다면, 그림과 같이 지형도를 그릴 수 있습니다. 이 모든 가중치 조합들에 대해서 손실은 특정 값을 찾게 될 텐데, 그래프에서는 z축이 되겠네요. 이 그림을 통해 두 가중치에 대해 손실이 얼마인지 봅시다.

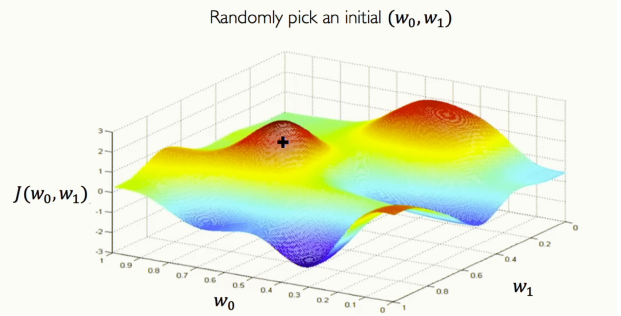
[그림 14] Loss Optimization

결국 가장 찾고 싶은 건 손실이 가장 낮은 지점입니다. 최적의 손실이죠. 그래프의 아무 지점에서 시작합니다. 그 지점에서 gradient, 즉 기울기 \(\frac{\partial J(W)}{\partial W}\) 를 계산합니다. 그 특정 지점에서 어느 방향이 기울없는지를 아주 국소적으로 추정하는 겁니다. 경사가 어디로 증가하는지, 혹은 감소하는지를 계산하고 반복하면, landscape를 따라 내려가면 국소 최소점을 찾을 수 있겠죠.

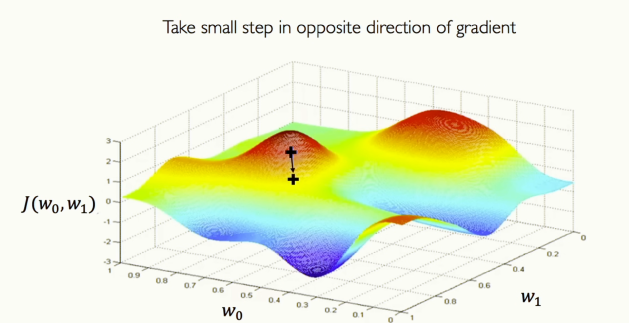
[그림 15] Loss Optimization

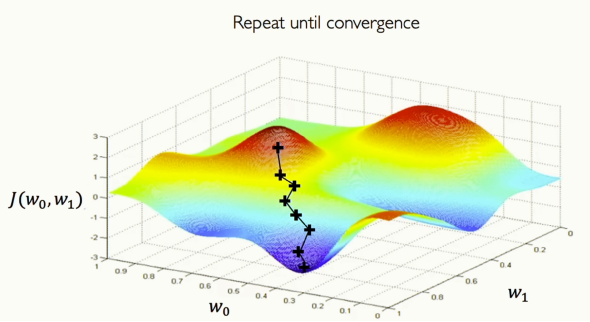
[그림 16] Gradient Descent

위에서 국소라는 표현을 썼죠? 이렇게 찾은 최소점이 손실 지형 전체에서 전역 최소점이 아닐수도 있습니다. 이러한 알고리즘을 Gradient Descent(경사 하강법)이라 부릅니다. 위에서 이야기한 알고리즘을 정리해서 적용하면 국소 최소점에는 쉽게 도달할 수 있습니다. 아래에 정리해봤습니다.

Gradient Descent Algorithm

Initialize weights randomly

가중치를 다음과 같이 랜덤 초기화합니다:

[ W \sim \mathcal{N}(0, \sigma^2) ]
Loop until convergence

수렴할 때까지 아래 단계를 반복합니다.
Compute gradient

손실 함수 ( J(W) ) 의 가중치 ( W ) 에 대한 그래디언트를 계산합니다:

[ \frac{\partial J(W)}{\partial W} ]
Update weights

학습률 ( \eta ) 를 이용해 가중치를 업데이트합니다:

[ W \leftarrow W - \eta \frac{\partial J(W)}{\partial W} ]
Return weights

최적화된 가중치 ( W )를 반환합니다.

코드로 이 부분을 보면 다음과 같습니다. Mit6s191 자료에는 텐서플로우 코드만 나와 있지만, numpy만을 이용해서 구현하는 방법과 파이토치로 이용해서 구현하는 방법도 소개해드리겠습니다.

### numpy 이용
import numpy as np

# Loss function (example)
def loss_function(W):
    return np.sum(W ** 2)

# Gradient of the loss function
def gradient(W):
    return 2 * W

# Gradient Descent Implementation
def gradient_descent(initial_weights, learning_rate, iterations):
    W = initial_weights
    for _ in range(iterations):
        grad = gradient(W)
        W = W - learning_rate * grad
    return W

### Pytorch 이용
import torch

# Initialize weights as a trainable tensor
weights = torch.randn(1, requires_grad=True)

# Learning rate
lr = 0.01

# Loop for Gradient Descent
while True:  # loop forever
    # Compute the loss
    loss = compute_loss(weights)  # Replace with your loss computation function
    
    # Compute gradients
    loss.backward()  # This computes dloss/dweights
    
    # Update weights
    with torch.no_grad():  # Disable gradient tracking for weight update
        weights -= lr * weights.grad
    
    # Clear gradients for the next iteration
    weights.grad.zero_()

### Tensorflow 이용
import tensorflow as tf

wights = tf.Variable([tf.random.normal()])

while True:
	with tf.GradientTape() as g:
		loss = compute_loss(weights)
		gradient = g.gradient(loss, weights)
	
	weights = wights - lr * gradient

결국 가장 중요한 것은 Gradient입니다. 그래디언트는 landscape에서 어느 방향이 위쪽인지 알려줄 뿐만 아니라 landscape가 어떤지, 손실이 모든 가중치의 함수로 어떻게 변하는지 알려줍니다. 그러면 도대체 이걸 어떻게 계산하는 걸까요? 이 과정을 backpropagation(역전파)라고 합니다. 같이 살펴보겠습니다.

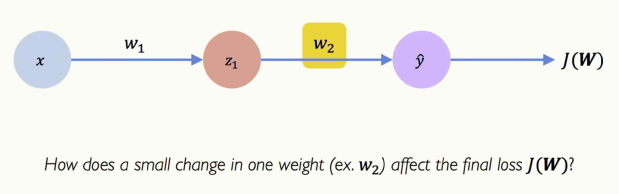
[그림 17] Computing Gradient: Backpropagation

가장 간단한 신경망부터 보겠습니다. 이 그림에서 가중치 W2에 대한 손실의 그래디언트를 계산하면 어떻게 될까요? W2의 작은 변화가 손실에 많은 영향을 미치게 됩니다. W2를 한 방향이나 다른 방향으로 조금 움직이면 손실이 올라가거나 내려가겠죠.

그럼 이 부분을 미분해보겠습니다. 손실에서부터 출력까지 역방향으로 연쇄 법칙(chain rule)을 적용하는 겁니다. 그러면 수식은 아래와 같아집니다.

\[\frac{\partial J(W)}{\partial w_2} = \frac{\partial J(W)}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial w_2}\]

여기서 W1의 그래디언트를 계산하기 위해 연쇄 법칙을 적용하면 아래 수식이 됩니다.

\[\frac{\partial J(W)}{\partial w_1} = \frac{\partial J(W)}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_1} \cdot \frac{\partial z_1}{\partial w_1}\]

관심 있는 가중치까지 연쇄 법칙을 이용해 거슬러 올라가고, 이 과정을 계속해서 반복하는 겁니다. 궁극적으로 출력에서 입력까지 원하는 값을 계산하는 겁니다.

수많은 레이어와 뉴런이 있으면 네트워크의 모든 가중치에 대한 작은 변화가 손실에 얼마나 영향을 미치는지 알 수 있습니다. 이러한 계산을 통해 손실을 개선하기 위한 신경망의 모든 가중치를 어떻게 면화시켜야 할지 정보를 전달합니다.

Neural Networks in Practice: Optimization

위에서 본 수식은 간단한 연쇄 법칙 그 이상도 아닙니다. 텐서플로우나 파이토치 같은 라이브러리는 이걸 굉장히 간단하게 사용하죠. 직접 구현할 필요 없지만 그래도 중요하기 때문에 직접 생각해보는 것은 중요합니다.

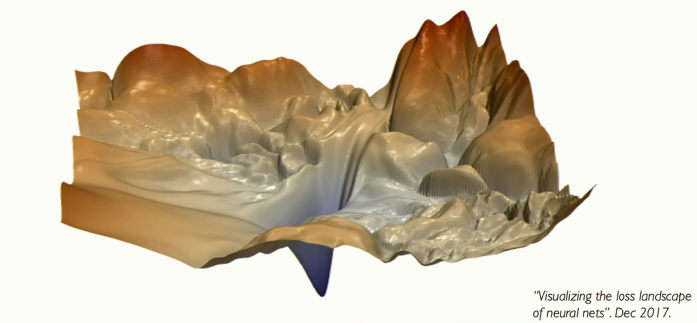
[그림 17] Training Neural Networks is Difficult

실제 신경망의 최적화는 위에서 본 것보다 훨씬 어렵고 수많은 계산이 소요됩니다. 위 그림은 유명한 그림입니다. 매우 깊은 신경망의 손실 지형을 시각화하려고 시도한 그림입니다. 실제 신경망은 2차원이 아니라 수백만 심지어 수십억 차원입니다. 그럼 이러한 손실 지도는 어떻게 보는 걸까요?? 이 사진을 공개한 논문은 기발한 아이디어로 그것을 시도해본 예시입니다. 결과가 굉장히 혼란스러워 보입니다. 이때 주의해야 할 점은 잘못된 위치에서 시작하면, 전역 최적해에 도달하지 못할수 있다는 것입니다. 그래서 초기화는 매우 중요한 과정입니다.

극솟값이 아니라 최솟값을 찾아야 하기 때문에 최적화하기 쉬운 손실 지형을 가지도록 신경망을 구성해야 합니다. 그렇기 때문에 그림의 손실 지형은 안 좋은 그림이고, 부드럽게 만들어야 합니다. 어떻게 할 수 있을까요?

\[W \leftarrow W - \eta \frac{\partial J(W)}{\partial W}\]

아까 본 이 수식에서 다루지 않은 매개변수가 있습니다. 바로 \(\eta\) 입니다. 학습률(Learning rate)이라고 불리는 이 변수를 어떻게 설정해야 할까요?

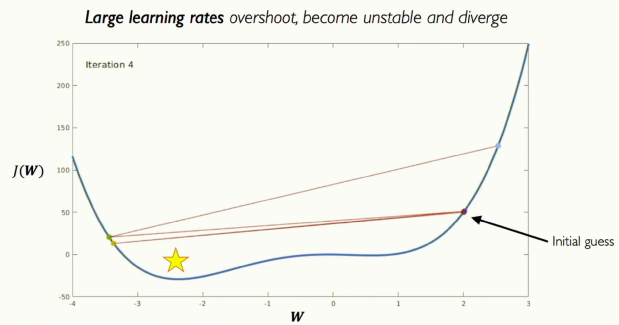
[그림 18] Setting the Learning Rate

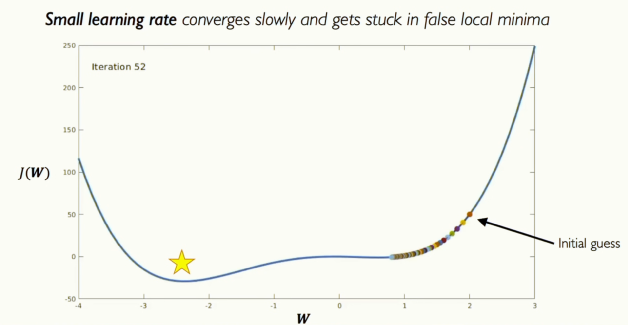
[그림 19] Setting the Learning Rate

그림에서 볼 수 있듯이, 학습률을 너무 크게 설정하면 손실이 발산해버리고, 너무 작게 설정하면 전역 최솟값이 아니라 국소 최솟값에 갇혀버립니다. 그러면 대체 이 변수를 어떻게 설정해야 할까요? 그 아이디어에 대해 생각해보겠습니다.

첫 번째 아이디어는 간단합니다. 그냥 다양한 학습률을 설정해보고, 어떤 것이 잘 작동하는지 보는 것입니다. 이 방법은 실제로 많이 쓰이는 방법입니다.😎

더 똑똑한 방법은 없을까요? 사실 학습률을 설정하는 데 사용되는 방법론은 굉장히 많습니다. SGD, Adam 등 Gradient Descent Algorithms들이 많이 있습니다. 어떤 Optimizer를 선택하할지 생각하는 것도 중요하고, 다영한 방법이 훈련 과정에 미치는 영향을 테스트 해보는 것도 중요합니다.

자세한 정보는 Optimizing Gradient Descent 링크를 통해 확인해보시면 될 것 같습니다.

Neural Networks in Practice: Mini-batches

계속 이야기 하고 있었던 경사하강법은 매우 계산 비용이 많이 듭니다. 전체 데이터셋의 모든 데이터 포인트에 대한 합계를 계산해야 하기 떄문입니다. (손실의 정의 얘기 했었죠? 모든 데이터 포인트의 평균이고, 모든 데이터 포인트의 기울기를 합산한다는 뜻이죠)

실질적으로 이것은 절대 불가능합니다. 데이터셋과 모델으 크기가 너무 커서 매 epoch마다 기울기를 계산할 수 없습니다.

그래서 새로은 경사 하강법 알고리즘인 SGD(Stochastic Gradient Descent)를 정의해보겠습니다. 이는 전체 데이터세트에 대한 기울기를 계산하는 대신에, 하나의 훈련 포인트를 선택하고 그 훈련 포인트의 기울기를 계산합니다.

Algorithm Steps

Initialize weights randomly

가중치를 다음과 같이 랜덤 초기화합니다:

[ W \sim \mathcal{N}(0, \sigma^2) ]
Loop until convergence

수렴할 때까지 아래 단계를 반복합니다:
1. Pick single data point
데이터셋에서 단일 데이터 포인트 ( i )를 선택합니다.
1. Compute gradient
선택한 데이터 포인트 ( i )에 대해 손실 함수의 그래디언트를 계산합니다:
[ \frac{\partial J_i(W)}{\partial W} ]
1. Update weights
학습률 ( \eta )를 이용해 가중치를 업데이트합니다:
```
 \[
 W \leftarrow W - \eta \frac{\partial J(W)}{\partial W}
 \]
```
Return weights

최적화된 가중치 ( W )를 반환합니다.

이 알고리즘은 기울기를 계산하는 것이 훨씬 쉬워지지만 불안정하다는 단점이 있습니다. 단일 예제로만 계산 되었기 때문에 매우 확률적입니다. 그럼 타협점은 뭘까요? 전체 데이터셋도 아니고 하나의 데이터 포인트가 아닌 데이터의 배치를 사용하는 겁니다. 이것을 미니배치라고 합니다.

보통 32개의 샘플의 기울기를 평균애어 기울기를 근사화 합니다. 여전히 불안정하지만 실제로 보통 괜찮은 결과가 나옵니다. 훨씬 간단하고, 보통 배치크기가 그렇게 크지 않기 때문에, 일반적인 GD보다 빠릅니다.

속도뿐만 아니라 기울기의 정확도도 솔루션에 빠르게 도달하는 중요한 요소입니다. 그렇기 때문에 SGD보다 미니배치를 사용하는 것이 더 정확하고 빠릅니다.

또다른 장점은 계산을 병렬화 할 수 있다는 점입니다. GPU의 다른 부분들이 데이터 포인트의 다른 부분을 처리할 수 있죠. 이렇게 하면 GPU 구조와 GPU 하드웨어를 사용하여 장점을 극대화 할 수 있습니다.

Neural Networks in Practice: Overfitting

이제는 신경망 학습 화정에서 겪는 다른 문제인 과적합(Overfitting) 문제에 대해 이야기해보겠습니다.

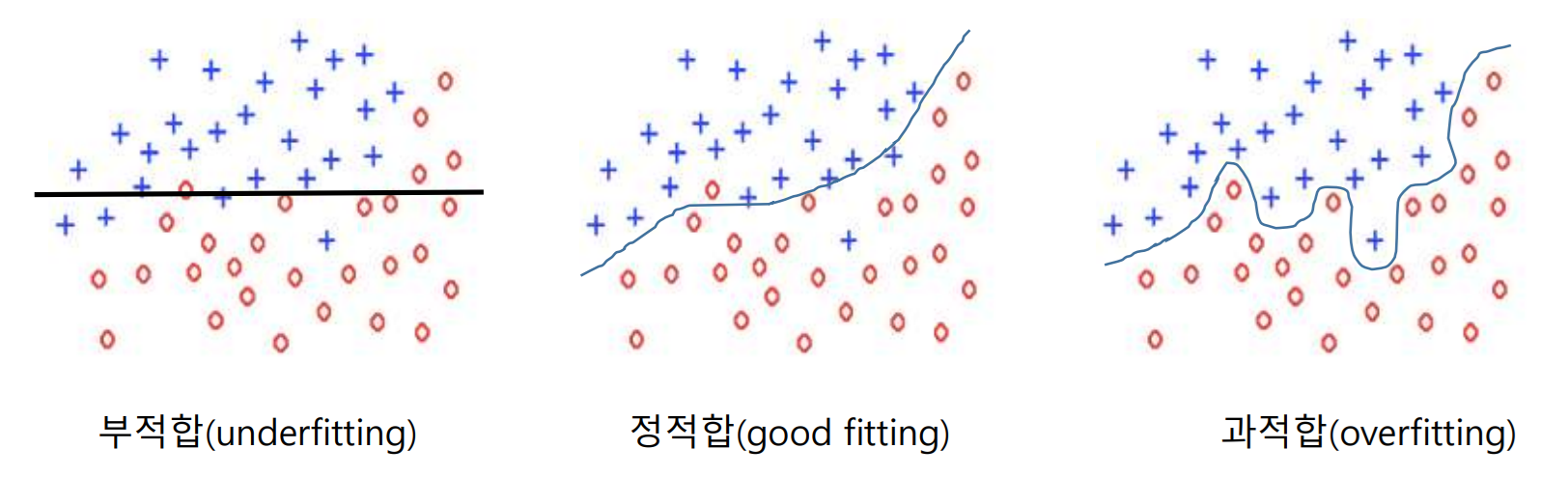
[그림 20] The Problem of Overfitting

과적합이란 신경망이 데이터셋에 너무 과하게 학습되어 제대로된 일반화를 하지 못하는 것입니다. 기본적으로 데이터셋은 방대하기 때문에, 그 데이터셋 중 노이즈같은 의미 없는 데이터가 많습니다. 그림에서와 같이 노이즈까지 학습을 해버리면 일반화가 되지 않는 거죠.

반대로 제대로된 학습이 안 되는 부적합도 있습니다. 보통 이는 충분한 학습 시간을 보장하면 해결됩니다.

그렇다면 어떻게 해야 과적합을 방지할 수 있을까요??

Dropout

과적합을 방지하는 방법은 정말 많습니다. 그 중에서 가장 먼저 떠오르는 방법은 Dropout입니다.

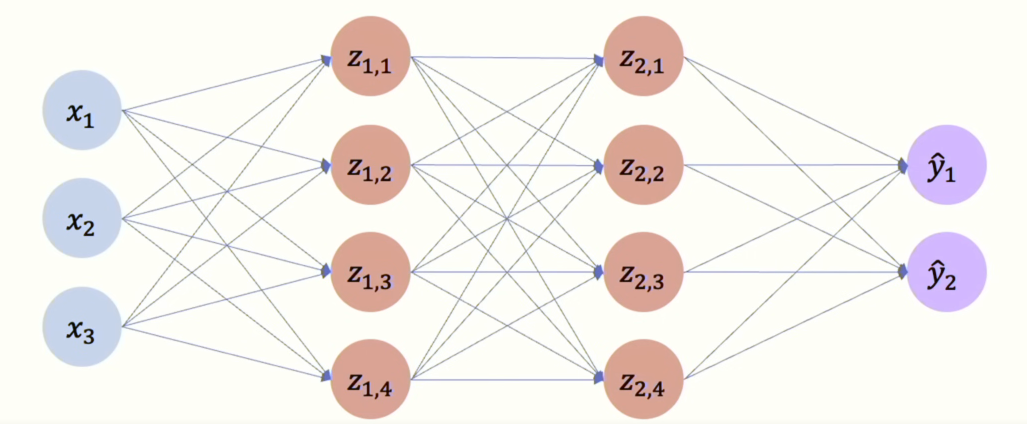
[그림 21] Dropout

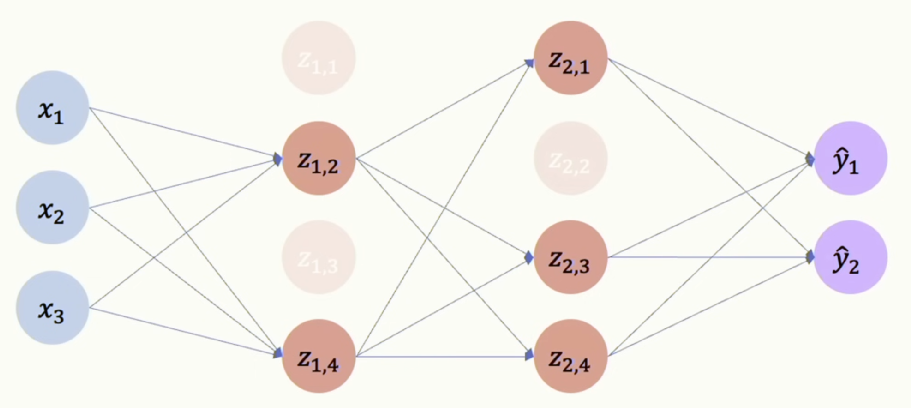
[그림 22] Dropout

[그림 21]과 같은 신경망을 학습할 때 무작위로 몇 개의 뉴런의 활성화 함수를 0으로 만들어서 [그림 22]와 같이 만듧니다. 일반적으로 50% 확률로 드롭아웃 레이어를 결정합니다. 매 에폭마다 드롭아웃 할 레이어를 무작위로 고르고, 추론할 때는 드롭아웃을 하지 않습니다. 코드로 구현할 경우 아래와 같이 간단하게 라이브러리로 구현할 수 있습니다.

# Tensorflow
tf.keras.layers.Dropout(p=0.5)

#Pytorch
torch.nn.Dropout(p=0.5)

Early Stopping

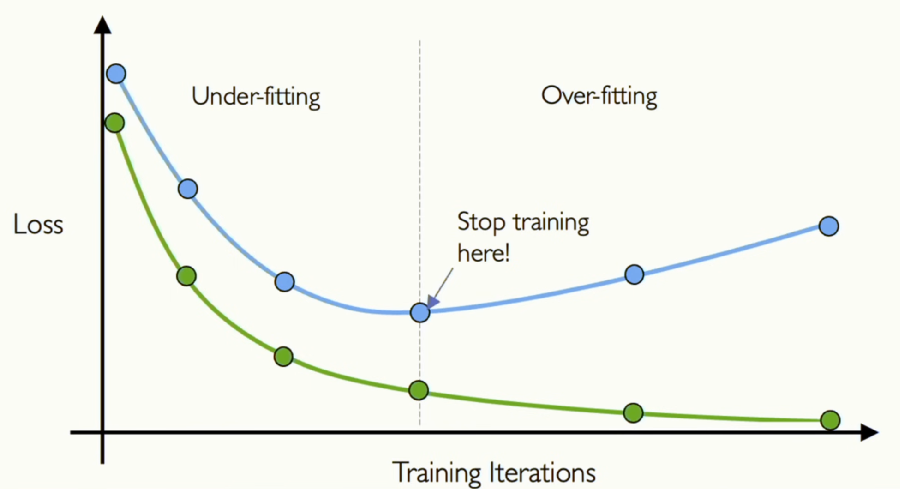
[그림 23] Early Stopping

두 번째 방법은 Early Stopping입니다. 보통 신경망을 훈련할 때 모든 데이터셋을 학습시키지 않습니다. 비율 설정은 자유지만, 보통 6:2:2 비율로 Train, Validation, Test 세 그룹으로 나눕니다.

Train 세트는 말그대로 직접적으로 훈련을 시킬 때 사용하는 데이터셋입니다. 계속 훈련을 하다보면 손실은 줄어들지만, 이는 과적합 될 위험성이 있습니다. 그래서 Validation 세트를 이용합니다.

Validation 세트는 직접적으로 학습에 적용되지는 않습니다. 하지만 이 Validation 데이터의 손실을 계산하여 그 추이를 봅니다. 그림과 Train세트와 Validation 세트가 동시에 감소하다가, Validation 세트의 손실이 올라가는 지점이 생깁니다. 이 부분이 학습 과정에서 일반화 되지 못하고 과적합 되고 있는 부분이므로 학습을 중지시킵니다.

여기까지 가장 기본적이고 기초적인 딥러닝 이야기, 그 중에서도 신경망 이야기를 해보았습니다. 딥러닝 시리즈 다음 게시글에는 기본적인, 유명한 신경망 모델들에 대해 이야기해보겠습니다😊