딥러닝 소개
by DINHO
안녕하세요!! 오늘부터 딥러닝 시리즈를 포스팅해볼까 합니다😏😏 이 시리즈의 글들은 MIT 6S191 수업을 바탕으로 정리한 글입니다. 출처를 남기지 않은 이미지는 이 수업 자료 이미지입니다. 오늘은 딥러닝이란 무엇인지!! 딥러닝에 대해 소개해보도록 하겠습니다.
What is Deep Learnig?
-
인공지능
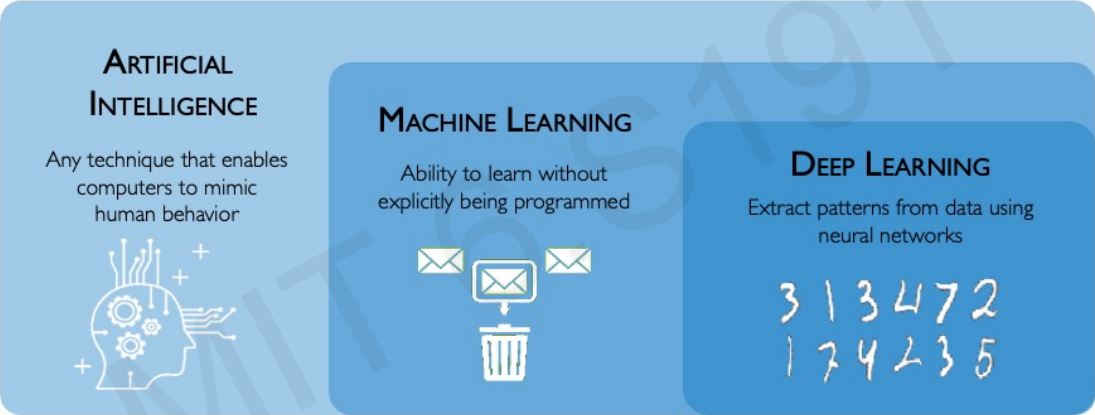
제가 인공지능 분야를 처음 공부할 때 가장 헷갈렸던 부분은 인공지능, 머신러닝, 딥러닝의 차이입니다.(사실 지금도 헷갈립니다…) 그래도 오늘 이 부분을 완전 정복해보겠습니다.
먼저 지능이란 뭘까요? 지능이란 정보를 처리하는 능력으로 정의할 수 있는데요. Artificial Intelligence, 인공지능이란 컴퓨터가 사람의 행동을 가능하게 만드는 모든 기술을 의미합니다. 그래서 극단적으로 말하면 계산기도 인공지능입니다!! 숫자 정보를 처리하여 사람이 계산하는 과정을 흉내내니까요!!
그렇다면 머신러닝은 뭘까요?? 인공지능과 머신러닝의 차이는 뭘까요??
-
머신러닝
일단 위 그림에서와 같이 머신러닝은 인공지능에 포함되는 개념입니다. 그렇다면 계산기는 머신러닝일까요?? 딱 봐도 아니죠? 머신러닝의 가장 큰 특징은 바로 학습에 있습니다.
머신러닝이란 “명확하게 프로그래밍하지 않고도 학습할 수 있는 능력”을 의미합니다. 다르게 말하면 데이터로부터 정보를 처리하고 의사결정하는 방법을 컴퓨터한테 가르치려는 과학 분야 입니다. 일반적으로 계산기에게 수식을 가르치진 않죠?? 그렇기 때문에 계산기는 머신러닝이 아닙니다.
그렇다면 딥러닝은 또 뭘까요??
-
딥러닝
딥러닝에서 가장 중요한 개념은 신경망(Neural Networks) 입니다. 딥러닝은 신경망을 사용하여 데이터에서 패턴 추출하고 학습합니다. 딥러닝이란 신경망을 사용해서 가공되지 않은 원시 데이터를 처리하고, 대규모 데이터 세트를 주입해서 향후 결정을 내릴 때 도우미 되게 하는 것이라고 말할 수 있습니다.
머신러닝과 딥러닝을 비교하기 위해 한 가지 예를 들어보겠습니다. 고양이와 강아지를 구분하는 인공지능 프로그램이 있다고 가정해봅시다. 머신러닝 프로그램은 인간이 개와 고양이의 특징을 추출하여 컴퓨터에게 알려주어야 합니다. 하지만 딥러닝은 대규모 데이터셋을 준비하기만 하면 신경망이 알아서 특징을 추출하고 학습합니다. 즉 머신러닝은 사람이 정의를 해야 하고, 딥러닝은 사람이 특징과 규칙을 설계하는 것에서 벗어납니다. 어떻게 감이 좀 잡히시나요??
최근 인공지능은 거의 대부분이 딥러닝을 사용합니다. 그에 대한 이야기를 해보겠습니다.
Why Deep Learning?
위에서 언급했듯이 머신러닝을 사용하게 되면 사람이 개입을 하게 됩니다. 수작업으로 엔지니어링한 기능은 시간이 많이 걸리고, 취약하며, 실제로 확장할 수 없습니다. 기본 특징을 데이터에서 직접 학습할 수 있을까요? 이렇듯 머신러닝의 단점을 보안하기 위해 딥러닝이 나왔습니다.
Why Now?
위에서 이야기한 딥러닝의 시초가 되는 이론들이 나온지는 굉장히 오래됐습니다. 기본이 되는 알고리즘인 Stochastic Gradient Descent는 1952년에 나왔고, 딥러닝의 필수 요소, Perceptron, 학습 가능한 가중치는 1958년에 처음 소개되었습니다. 오래 전부터 연구가 되었는에 왜 지금 인공지능이 부상하고 있을까요? 크게 세 가지 이유가 있습니다.
-
Big Data
이미지 출처:https://www.linkedin.com/pulse/title-demystifying-big-data-unveiling-power-analytics-shruti-kashyap- 가장 먼저 데이터셋이 많아졌습니다. 현재 인공지능에서는 많은 양의 데이터셋을 확보하는 것이 중요합니다. 최근에는 데이터셋의 종류도 많아지고 수집과 저장이 쉬워졌기 때문에 인공지능이 부상할 수 있습니다.
-
Hardware

이미지 출처:https://www.nvidia.com/ko-kr/data-center/h100/ 두번째 이유로는 하드웨어의 발달, 그 중에서도 GPU의 발달입니다. 빅데이터를 수집한다 하더라도 거대한 양의 데이터셋을 처리하는 데 계산량은 상상을 초월합니다. 그런데 GPU가 이를 해결해줍니다. GPU는 병렬 처리 계산이 가능해서 거대한 양의 데이터셋도 빠르게 계산이 가능합니다. (그래서 NVIDIA의 주식이 엄청나게 오른 것입니다.)
-
Software
마지막으로 소프트웨어의 발달입니다. 기술이 발전하면서 새로운 모델들이 계속 나오고 있고, TensorFlow나 Pytorch 같은 라이브러리가 잘 발달 되면서 인공지능 모델을 코딩하는 데 수고가 덜 해졌습니다.
위 세 가지 종합적인 요소들이 겹치면서 최근 인공지능 개발 분야가 급부상하고 있는 겁니다.
여기까지 인공 지능, 머신러닝, 딥러닝에 대해 소개했습니다. 그렇다면 본격적으로 신경망(Neural Network) 에 대해서 이야기해보겠습니다!!
Perceptron
먼저 퍼셉트론(Perceptron)이란 딥러닝의 구조적인 구성요소입니다. 퍼셉트론은 정확히 뉴런(Neuron)의 개념과 일치합니다. 딥러닝 공부를 하다 보면 퍼셉트론이라는 용어보다는 뉴런이라는 용어를 더 많이 볼 텐데요, 둘 다 똑같은 거라고 보시면 됩니다.(이제부터 저는 뉴런이라고 하겠습니다.)
모든 신경망은 여러 개의 뉴런으로 구성되어 있습니다. 뉴런은 전(前)방향 전파입니다.
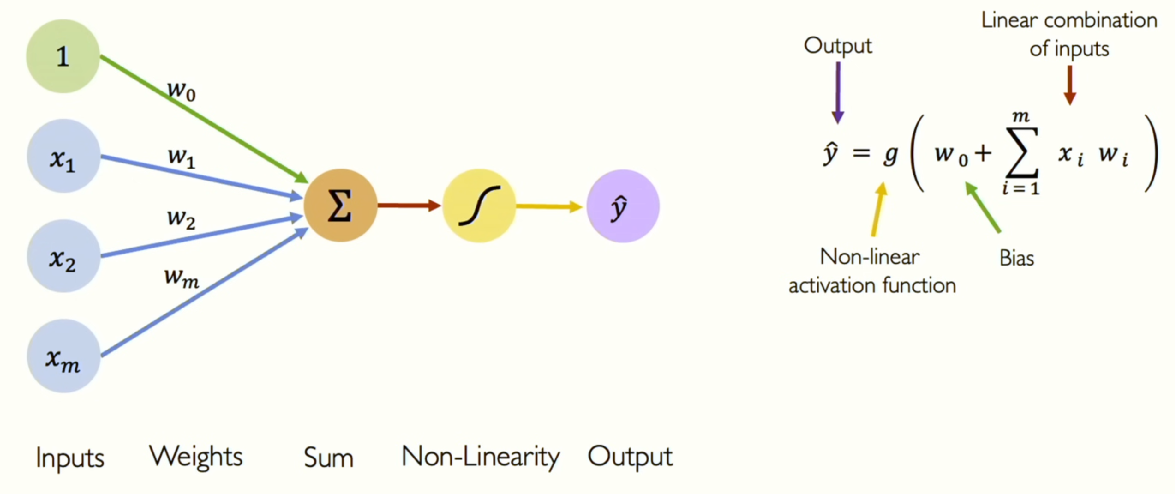
뉴런은 여러 개의 정보를 받아들일 수 있습니다. 그림에서는 \(x_{1},x_{2},x_{m}\) 입니다. 바로 입력들의 집합이죠.
각 입력은 특정 가중치와 요소별로 곱해집니다. 각 입력마다 해당하는 가중치가 있으며, 이 가중치들이 입력에 할당된다고 생각하면 됩니다. 그림에서는 \(w_{0},W_{1},W_{m}\) 등이 가중치입니다.
이제 모든 입력 값을 할당된 가중치와 곱한 후 그 결과를 모두 더합니다. 이렇게 더한 하나의 숫자를 비선형 활성화 함수(Non-linear activation function)에 통과시킵니다. 함수를 통해 출력 되는 아웃풋을 y라고 하겠습니다.
그런데 제가 언급을 안 한 것이 있습니다. 그림에서는 1에 해당하는 부분인데요, 이것은 바이어스입니다. 이 바이어스는 뉴런이 활성화 함수를 x축을 따라 수평으로 이동시킬 수 있게 해줍니다.
글로 말한 모든 과정이 수식 한 줄로 정리 됩니다. 여기에 선형대수학을 적용하여 수식을 다시 쓸 수 있습니다.
\[\widehat{y} = g(w_{0} + X^{T}W)\]where: \(\mathbf{X} = \begin{bmatrix} x_1 \\ \vdots \\ x_m \end{bmatrix} \quad \text{and} \quad \mathbf{W} = \begin{bmatrix} W_1 \\ \vdots \\ W_m \end{bmatrix}\)
X는 입력 값을 담은 벡터이고 W는 가중치를 담은 벡터입니다. 내적은 원소별 곱셈을 하고, 그 곱셈 결과를 모두 더하는 과정이므로 입력값은 X와 W의 내적으로 표현할 수 있습니다. 그리고 바이어스 항을 더해줍니다. 여기에 비선형 활성화 함수 g를 적용해주면 출력 y를 얻을 수 있습니다. 간단한 선형대수 내용이므로 어렵지 않습니다.
이제 여기서 활성화 함수가 실제로 무엇을하는지 더 자세히 알아보겠습니다.
Activation Functions
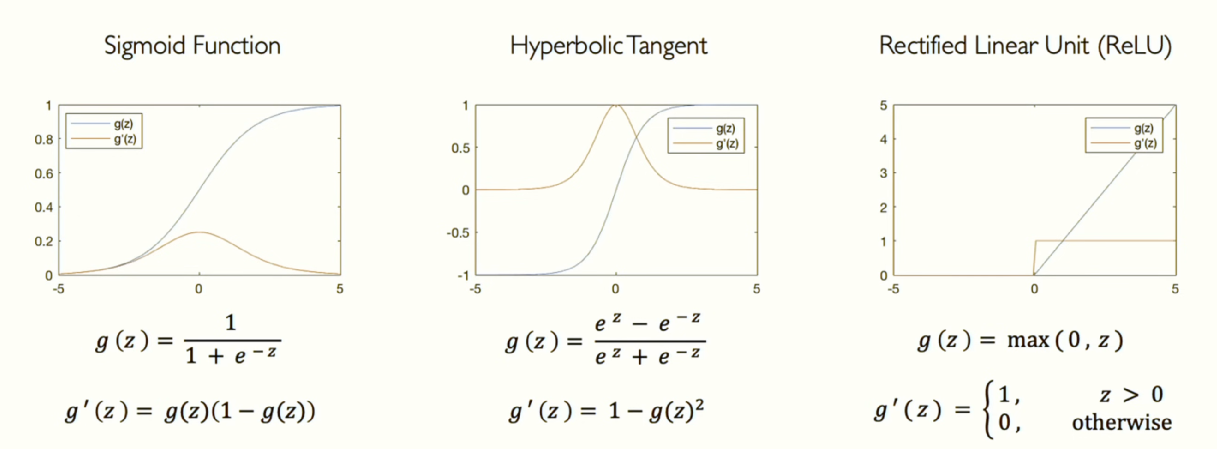
지금까지 계속해서 활성화 함수는 비선형 함수라고 했습니다. 그림은 활성화 함수의 예시입니다. 가장 대표적인 활성화 함수 중에는 sigmoid(시그모이드)가 있습니다. 시그모이드가 자주 사용되는 이유는 입력값이 x축에서 어떤 실수든 받을 수 있기 때문입니다. 하지만 y축에서는 모든 입력 x를 0과 1로 압축합니다. 그래서 답을 확률로 변환하거나 확률 분포로 나타내고자 할 때 많이 사용됩니다. 확률 분포를 학습하도록 뉴런을 가르치는 데 자주 사용됩니다.
그 외에도 다양한 종류의 비선형 활성화 함수들이 사용됩니다. 위 그림은 대표적인 활성화 함수의 예시들이고 TensorFlow를 이용하여 쉽게 사용할 수 있습니다.
맨 오른 쪽의 ReLU(Rectified Linear Unit)은 가장 인기있는 활성화 함수 입니다. 기본적으로 x=0에서의 비선형성을 제외하면 모든 곳에서 선형적인 함수입니다. 이 함수의 장점은 계산이 매우 쉽습니다. 단지 두 개의 선형 함수를 조각별로 결합했기 때문입니다. 이 함수는 우리가 필요로 하는 비선형성을 가지고 있습니다.
그런데 왜 비선형성이 필요할까요?? 답은 간단합니다. 비선형 데이터를 다루기 위해서입니다. 활성화 함수의 목적은 네트워크에 비선형성을 도입하는 것입니다. 즉 신경망이 비선형 데이터를 다룰 수 있게 만드는 것입니다.
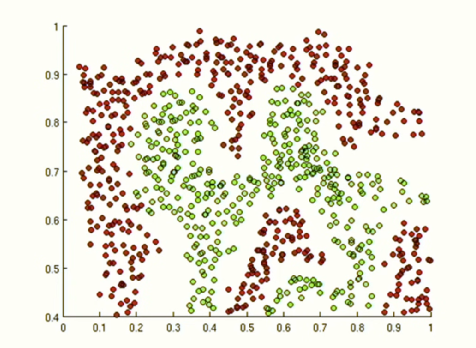
위 그림을 예시로 보겠습니다. 만약 위 그래프에서 초록색과 빨간색 점들을 구분할 수 있는 신경망을 만든다고 가정해보겠습니다. 죽었다 깨어나도 선형 함수로는 이 데이터를 구분할 수 없습니다.
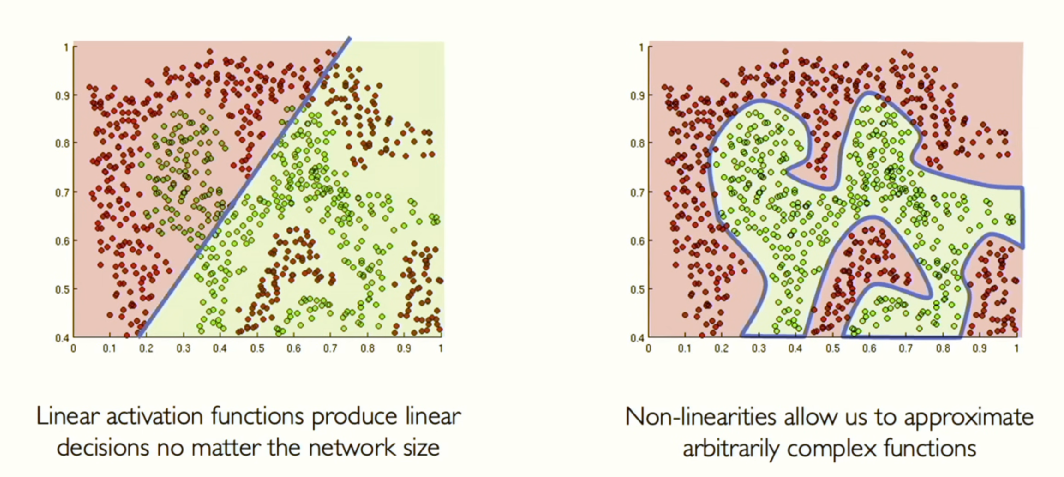
이 그림에서 선형 함수로 빨간 점과 초록 점을 구분한다고 하면 신경망이 아무리 커도 왼쪽 그림이 최선입니다. 하지만 비선형 함수를 추가하면 적은 신경망으로도 표현력이 좋아지고 오른쪽 그림과 같이 데이터 집합의 더 많은 복잡성을 포착할 수 있게 됩니다. 이것은 곧 신경망이 훨씬 더 강력해질 수 있게 만들어줍니다. 예시와 함께 살펴보겠습니다.
Example
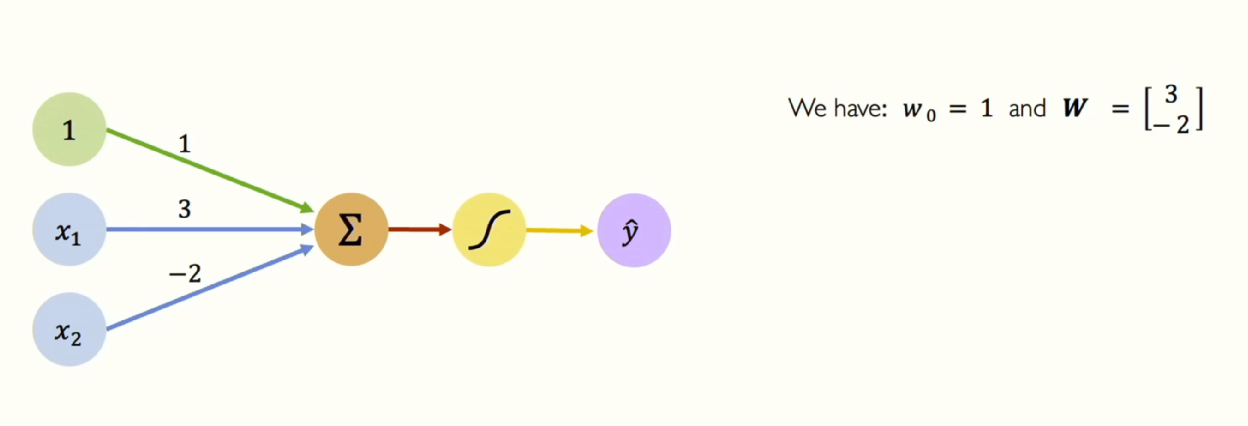
여기 학습된 신경망이 있다고 가정합시다. 학습된 신경망이라는 것은 가중치가 주어졌다는 뜻입니다. 입력뿐만 아니라 이 신경망의 가중치가 무엇인지 알려져 있는 겁니다. 여기서 바이어스는 1이고 가중치 벡터 W는 (3,-2)입니다. 이 신경망에는 두 개의 입력 \(x_{1}, x_{2}\) 가 있습니다. 이제 이 신경망의 출력을 얻고 싶다면 어떻게 하면 될까요?? 위에서 주구장창 이야기 했었죠?? 입력과 가중치의 내적을 계산하고, 바이어스를 더한 다음, 비선형 활성화 함수를 적용하는 것 입니다. 오늘 포스팅에서 이 진한 글씨만 알고 가도 90퍼센트 성공입니다.
이렇게 계산하고 나면 뉴런은 하나의 숫자를 출력하게 되겠죠. 그렇다면 그 비선형성 안에 무엇이 있을까요? 아래 식(아까 봤던 식입니다.)을 보면 알 수 있듯이 단순히 입력들과 가중치들의 가중 조합입니다. 이것은 하나의 숫자를 만들어냅니다.
\[\hat{y} = g \left( w_0 + \mathbf{X}^T \mathbf{W} \right) \\ = g \left( 1 + \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}^T \begin{bmatrix} 3 \\ -2 \end{bmatrix} \right) \\ \hat{y} = g \left( 1 + 3x_1 - 2x_2 \right)\]하지만 실제로, 이 모델이 볼 수 있는 어떤 입력에 대해서도, 이 모델은 두 개의 파라미터가 있기 때문에 이것은 사실 2차원 직선입니다. 이것을 아래와 같이 그릴 수 있습니다. 우리는 이 뉴런이 x1과 x2 사이의 축에서 어떻게 점들을 구분하는지 정확히 볼 수 있습니다. 이 때 그 뉴런에 새로운 데이터 포인트를 준다면, 그 점이 2차원 공간에 직선의 어느 쪽에 떨어지느냐에 따라 우리에게 답이 달라집니다.
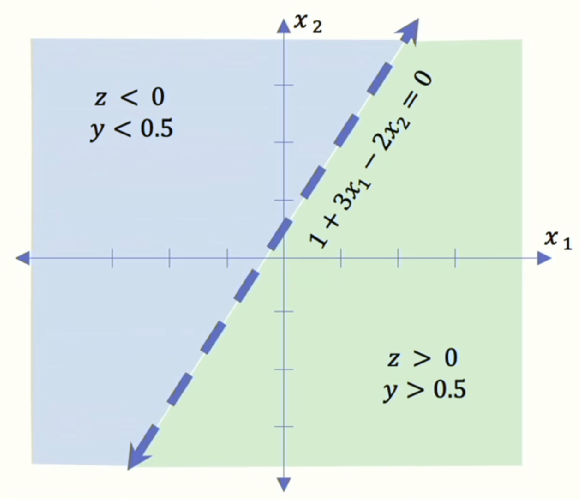
여기서 활성화 함수로 시그모이드를 썼다고 가정합시다. 시그모이드 함수의 범위는 0에서 1사이의 값을 가지지만, 암묵적으로 0.5보다 작은 모든 것과 0.5보다 큰 모든 것을 나눕니다. 그래서 x가 직선의 어느쪽이냐에 따라 정확히 두 부분으로 나눠집니다. 여기서 우리는 이 공간을 시각화할 수 있으며, 이것을 신경망의 feature space라고 합니다.
여기까지 본 뉴런은 굉장히 단순한 뉴런이었습니다. 그런데 사실, 앞으로 우리가 진짜로 다루게 될 뉴런과 신경망의 종류는 수백만, 심지어 수십억 개의 입력 파라미터를 가지고 있을 겁니다. 그래서 방금과 같이 feature space를 시각화 하는 것은 불가능에 가깝습니다. 하지만 그럼에도 위 내용을 통해 뉴런, 즉 퍼셉트론의 직관을 어느 정도 가지게 될 수 있을 겁니다.
다음에는 신경망을 만들면서 이 모든 것이 어떻게 함께 작동되는지 살펴보겠습니다.
Follow my github