최근 오디오 생성형 AI 모델에 대한 연구가 활발히 진행중입니다. 그 중에서도 가장 최신 모델인 Auffusion과 AudioLDM2에 대한 논문을 보았는데요. 각 모델에 대한 자세한 정보는 링크를 타고 들어가시면 볼 수 있습니다.

두 모델 모두 Diffusion, HiFi-GAN, Transformer, VAE 등 공통적으로 알아야할 내용들이 있습니다. 그래서 이번 게시글에서는 먼저 공통적으로 알아야할 내용중 Diffusion에 대해 다루어보겠습니다. 추후에 두 모델의 구조와 차이에 대해서 게시해보겠습니다. 이번 글은 수식이 많고 어려울 수 있습니다🙄🙄

이 두 논문에서는 Latent Diffusion Model(LDM)을 사용하므로 Latent(Stable) Diffusion에 대해 알아보겠습니다.

  1. Diffusion Overview

    디퓨젼(Diffusion)이란 데이터를 만들어내는 Deep Generative Model 중 하나입니다.

    이미지 출처: https://miro.medium.com/v2/resize:fit:720/format:webp/1*xc2Y6jwIUhfEGxJLytU1RA.png

    Latent Diffusion Model(LDM)에서는 입력 값으로 픽셀값 x가 아닌 Latent Embedding z가 들어가기 때문에 제가 설명할 때는 입력을 z로 설명하겠습니다.

    그림에서와 같이 디퓨젼(Diffusion)에는 Forward process와 Reverse process가 있습니다. Forward process에서는 데이터에 Fixed(고정된) Gaussian Noise가 더해집니다. Reverse process에서는 데이터를 Learned(학습된) Gaussian Noise로 뺍니다. 즉, 디퓨젼(Diffusion)의 목적은 Forward -> Reverse 단계를 거친 ‘결과 이미지’를 ‘입력 이미지’의 확률 분포와 유사하게 만드는 것입니다. 이미지 픽셀값에 첨가된 Noise 값을 계산할 수 있다면 Noise 이미지 \(z_T\) 로부터 진짜 이미지 \(z_0\)로 되돌리는 것이 가능하겠죠? 이 말은 곧 입력으로 랜덤하게 생성한 Noise 이미지 \(z_T\)가 들어가면 Reverse Diffusion process를 거쳐 완전한 이미지 \(z_0\)가 만들어진다는 의미입니다.

    그렇다면 과정들을 자세하게 알아보도록 하겠습니다.

  2. Forward process

    Forward process에서는 노이즈의 분포를 알아내야 합니다. 그 이유는 Reverse process에서 학습할 때 Forward process의 정보를 활용하기 때문이죠. Forward process는 데이터 \(z_0\) 에서 잠재 변수(latent variable) \(z_T\) 까지의 고정 마르코프 체인(Fixed Markov Chain)으로 정의됩니다. 이를 수식으로 표현하면 다음과 같습니다.

    \[q(z_1,z_2, ... , z_T \vert z_0) = \prod_{t=1}^{T} qz_t \vert z_{t_1})\]

    각 부분을 살펴보면

    \(q(z_1,z_2, ... , z_T \vert z_0)\) : 이 수식은 원본 데이터 \(z_0\) 가 주어졌을 때, 노이즈를 추가하여 \(z_1\) 부터 \(z_T\) 까지 연속적인 상태에 도달할 조건부 확률을 나타냅니다.

    \(\prod_{t=1}^{T}\) : 이 수식은 다들 아실 텐데요!! t=1 부터 T까지의 모든 항목을 곱하라는 의미입니다. 시그마의 곱셈버전이라고 생각하시면 편합니다.

    \(q(z_t \vert z_{t_1})\) : 이 수식은 각 단계 t에서의 상태 \(z_t\) 가 이전 상태 \(z_{t-1}\) 에 기반할 때의 확률 분포를 나타냅니다.

    요약하자면 이 수식은 노이즈가 점차적으로 추가되는 과정을 수학적으로 모델링한 것입니다. 각 단계에서의 변화는 조건부 확률 분포를 사용하여 표현되며, 전체 Forward process는 이러한 변화들의 연속적인 곱으로 나타납니다.

    \(q(z_t \vert z_{t_1})\) 이 수식은 다음과 같이 알아볼 수 있습니다.

    \[q(z_t \vert z_{t-1}) := \mathcal{N}(z_t; \sqrt{1 - \beta_t}z_{t-1}, \beta_t I)\]

    각 부분을 살펴보면

    \(\mathcal{N}(z_t; \sqrt{1 - \beta_t}z_{t-1}, \beta_t I)\) : 여기서는 평균이 \(\sqrt{1 - \beta_t}z_{t-1}\) , 공분산이 \(\beta_t I\) 인 다변수 정규 분포를 의미합니다. 여기서 \(I\)는 단위 행렬(identity matrix)을 의미하며, 이는 모든 변수들이 서로 독립적이고 동일한 분산을 가짐을 의미합니다.

    \(\sqrt{1 - \beta_t}z_{t-1}\) : 여기서 \(\sqrt{1 - \beta_t}\) 는 이전 상태 \(z_{t−1}\) 에 노이즈를 추가하기 전에 적용되는 스케일링 팩터(scaling factor)입니다. 이는 디퓨젼(Diffusion) 과정에서 각 단계에서 이전 상태 \(z_{t−1}\) 에 노이즈를 추가ㅏ하기 전에 적용되는 배율을 의미합니다. 스케일링 펙터의 역할에는 정보의 보존, 노이즈 추가의 조절, Reverse process 준비 등이 있습니다. 자세히 설명하자면:

    • 정보의 보존: 스케일링 팩터는 원본 데이터 \(z_{t−1}\) 에서 일부 정보를 유지하면서 새로운 노이즈를 추가합니다. 이때, \(\beta_t\) 가 0에 가까울수록 더 많은 원본 정보를 유지하며, 1에 가까울수록 더 많은 정보가 노이즈로 인해 손실됩니다.

    • 노이즈 추가의 조절: 디퓨젼(Diffusion) 모델은 데이터에 점차적으로 노이즈를 추가하여 데이터 분포로부터 멀어지게 만드는 과정입니다. 스케일링 팩터는 각 단계에서 노이즈를 추가할 때 원본 데이터의 양을 조절하여 이 과정을 세밀하게 제어합니다.

    • Reverse process 준비: 스케일링 팩터는 forward process에서 데이터에 노이즈를 추가하는 방식을 정의함으로써, 나중에 Reverse process를 수행할 때 데이터를 복원하는 방법을 모델이 학습할 수 있도록 준비합니다.

    \(\beta_t I\) : 이는 추가되는 노이즈의 분산을 정의합니다. \(\beta_t I\) 는 각 단계에서 추가되는 노이즈의 양을 제어하는 매개변수로, 시간에 따라 변할 수 있습니다.

    전체 절차는 미리 결정된 노이즈 스케줄 “β1,…,βT”에 따라 초기 잠재 데이터 \(z_0\) 를 노이즈 잠재 변수 \(z_T\) 로 변환합니다. 여기서 βt는 작은 양의 상수입니다. \(q(z_t \vert z_{t−1})\) 은 \(z_{t−1}\) 의 분포에 작은 가우스 노이즈가 추가되는 함수를 나타냅니다. 이 수식은 모델이 이전 상태 \(z_{t−1}\) 로부터 새로운 상태 \(z_T\) 를 생성할 때, 원본 데이터의 일부 정보를 유지하면서 어느 정도의 노이즈를 추가할지를 정의합니다. 디퓨젼(Diffusion) 과정에서는 이처럼 점차적으로 노이즈를 증가시키며, 원본 데이터로부터 멀어지는 과정을 시뮬레이션합니다.

  3. Reverse process

    Reverse process에서는 위에서 언급한 것처럼 가우시안 노이즈가 있는 \(z_T\) 에서 샘플을 복구하는 것을 목표로 합니다. 학습 가능한 매게 변수 \(\theta\) 를 사용하여 잠재 변수(latent variable)를 \(z_T\) 에서 \(z_0\) 로 변환합니다. 이를 수식으로 표현하면 다음과 같습니다.

    \[p_{\theta}(z_0, \ldots, z_{T-1}\vert z_T) := \prod_{t=1}^{T} p_{\theta}(z_{t-1}\vert z_t)\]

    각 부분을 살펴보면

    \(p_{\theta}(z_0, \ldots, z_{T-1}\vert z_T)\) : 이 식은 모델 매개변수 \(\theta\) 를 사용하여, 가장 노이즈가 많은 \(z_T\)로 시작해서 원본 데이터 \(z_0\) 까지 역으로 추적하는 전체 확률 과정을 나타냅니다.

    \(\prod_{t=1}^{T}\) : 이 호는 각 시간 단계 t에 대해 노이즈를 제거하는 단계별 확률 \(p_{\theta}(z_{t-1}\vert z_t)\) 들의 곱을 나타냅니다. 즉, 이 식은 전체 Reverse process가 각 단계별로 연속적으로 노이즈를 제거해 나가는 곱셈 과정임을 표현합니다.

    \(p_{\theta}(z_{t-1}\vert z_t)\) 이 수식은 다음과 같이 알아볼 수 있습니다.

    \[p_{\theta}(z_{t-1}\vert z_t) := \mathcal{N}(z_{t-1}; \mu_{\theta}(z_t, t), \Sigma_{\theta}(z_t, t))\]

    즉 이 수식은 \(z_T\) 가 주어졌을 때 다음 상태 \(z_{t−1}\) 의 확률 분포를 나타내는 조건부 확률 분포입니다.

    \(\mu_{\theta}(z_t, t)\) 는 평균 벡터를, \(\Sigma_{\theta}(z_t, t)\) 는 공분산 행렬을 나타내며, 모델의 매개변수 θ에 의존합니다. 이 매개변수들은 모델이 학습 과정에서 최적화합니다.

    결론적으로 디퓨젼(Diffusion) 모델은 이와 같은 reverse process를 통해, 노이즈가 첨가된 데이터로부터 원본 데이터를 복원하는 방법을 학습합니다.

  4. 구조

    위에 글을 잘 읽고 따라 오셨다면 디퓨젼(Diffusion) 모델이 어떤 과정으로 진행되는지 감을 잡으셨을 겁니다. 그렇다면 디퓨젼(Diffusion)이 어떤 구조로 되어 있는지 알아보겠습니다.

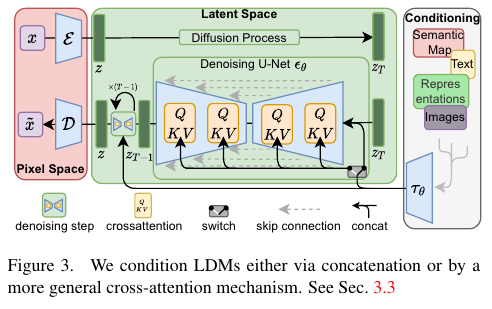    이미지 출처: Rombach & Blattmann, et al. 2022

    그림과 같이 디퓨젼(Diffusion) 모델은 U-Net구조를 하고 있습니다. 이는 U-Net이 Input과 동일한 Resolution(해상도)의 Output을 내기 적합하기 때문입니다. 아울러 U-Net에서 \(\tau\) 와 Condition(텍스트나 이미지 등등)을 별도로 입력 받습니다. 이렇게 입력된 Condition은 Diffusion Model 내부에서 Cross Attention 연산을 사용하여 적용됩니다.

  5. Loss function

    마지막으로 Diffusion의 Loss function에 대해 알아보겠습니다. Loss function의 역할을 간단하게 요약하면 다음과 같습니다.

    • 성능 측정: Loss function은 모델의 성능을 측정하는 기준입니다. 낮은 손실(loss) 값은 모델이 데이터를 잘 예측하고 있다는 것을 의미하며, 높은 손실 값은 모델의 예측이 부정확하다는 것을 나타냅니다.

    • 훈련 방향 제시: Loss function은 모델의 학습 방향을 제시합니다. 모델은 Loss function의 값을 줄이는 방향으로 매개변수를 업데이트하게 됩니다.

    • 경사 하강법: 대부분의 최적화 알고리즘은 경사 하강법(gradient descent)을 사용하여 Loss function의 최소값을 찾습니다. 이는 Loss function의 기울기(미분값)를 계산하여, 기울기가 낮아지는 방향으로 매개변수를 조정합니다.

    Loss function은 여러 가지를 고려하여 선택해야 합니다. 회귀, 분류, 구조 예측 등 문제 유형에 따라 적합한 Loss function을 고려해야 하고, 데이터의 특성과 분포에 따라 MSE, MAE 등 알맞은 방법을 선택해야 합니다. 제가 설명하는 Loss function은 Auffusion에서 제시한 Loss function입니다. 읽고 계신 논문이 따로 있으시다면 그 논문에서 이야기하는 Loss function을 참고하시면 좋을 것 같습니다.

    \[\mathcal{L}_{\theta} = \|\epsilon_{\theta}(z_t, t, \tau) - \epsilon\|_2^2\]

    이 논문의 Diffusion 모델에서 Loss function은 텍스트 프롬프트 \(\tau\) 를 사용하여 오디오 신호의 픽셀 분포 \(z_0\) 를 구성하는 과정에서 U-Net 기반의 디퓨전 모듈을 미세 조정(fine-tune)할 때 사용됩니다. \(\epsilon_{\theta}(z_t, t, \tau)\) 는 텍스트 안내 τ를 위한 U-Net으로 구성된 텍스트 안내 Denoising(노이즈 제거) 네트워크입니다. 이 네트워크는 U-Net구조와 텍스트에 대한 크로스-어텐션(cross-attention) 구성요소를 포함하고 있습니다. \(z_t\) 는 노이즈가 섞인 데이터를, t는 랜덤한 시간 스텝을 의미합니다.

    \(\epsilon\) 은 표준 정규 분포 \(\mathcal{N}(0,I)\) 에서 추출된 가우시안 노이즈입니다. Loss function \(\mathcal{L}_{\theta}\) 는 노이즈 공간에서의 평균 제곱 오차(Mean Squared Error, MSE)를 최소화하는 것을 목표로 합니다. 다시 말해, 모델이 생성한 디노이징 결과와 실제 노이즈 사이의 차이의 제곱을 최소화하려는 것입니다.

여기까지 Diffusion에 대한 내용입니다. 이번 글이 굉장히 어렵습니다. 천천히 여러번 읽는 것을 추천드립니다. 아울러 수식을 직접 입력했기 때문에 오타가 있을 수 있습니다. 이 글은 LDM관련 논문을 읽을 때 참고용으로 적합할 것 같습니다. 다음에는 HiFi-GAN에 대해서 알아보도록 하겠습니다.

긴 글 읽어주셔서 감사합니다.😊😊