지난번에 이어서 “Mathad, Vikram C., et al. “A deep learning algorithm for objective assessment of hypernasality in children with cleft palate.” IEEE Transactions on Biomedical Engineering 68.10 (2021): 2986-2996.” 논문 리뷰를 이어서 하겠습니다.

지난번 논문 리뷰1에서는 구개열(Cleft Palate)과 구강, 비강 조음들을 알아보았는데요. 이번에는 본격적으로 데이터셋이나 어떤 구조의 DNN 모델인지 알아보도록 하겠습니다😀😀 아울러 이번 글에서 MFCC라는 전처리 특징이 언급되는데요. 이부분에 대한 설명은 제 블로그 신호-처리-이론 카테고리에서 추후에 다루어보도록 하겠습니다😊😊👍👍

DATABASES

1. Healthy Speech Corpus

   먼저 이 논문에서는 Librispeech 데이터베이스를 이용해서 100 시간 동안 건강한 사람들의 발음을 DNN을 이용해서 학습시켰습니다. 데이터베이스에는 성인 251명(남자 125명, 여자 126명)이 녹음한 영어 음성 샘플이 포함되어 있습니다.

2. Americleft Database

   Americleft Database는 구개열(Cleft Palate, CP)이 있는 어린이 60명(남자 37명, 여자 23명)과 정상 발음 어린이 10명(남자 6명, 여자 4명)의 음성 샘플이 포함되어 있습니다.

3. NMCPC Dateabase

   NMCPC 데이터베이스는 평균 연령 9.2 ± 3.3세의 대조군 10명(남자 8명, 여자 2명)과 CP 아동 41명(남자 22명, 여자 19명)의 미국 영어 음성 샘플로 구성됩니다. NMCPC 데이터베이스는 뉴멕시코 구개열 센터의 Luis Cuadros 박사에게 요청하면 얻을 수 있는 공개적으로 사용 가능한 데이터베이스입니다.

METHODS

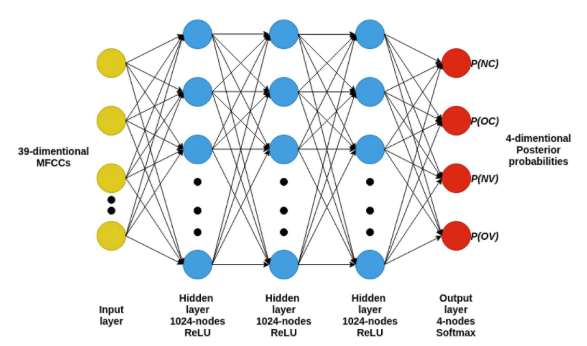Fig3

그림 3은 NC, OC, NV, OV를 분류하기 위한 DNN 모델입니다.

모델 구조

이 모델은 39차원 MFCC 입력 레이어, 각 레이어에 1024개의 히든 레이어(Hidden Layer), 4차원 소프트맥스 출력 레이어로 구성된 feed-foward 신경망입니다. 출력 레이어는 NC, OC, NV, OV에 해당하는 사후 확률을 생성합니다.(사후확률이 무엇인지 추후에 기회가 되면 다루어보도록 하겠습니다😁)

DNN 학습

먼저 Librispeech 데이터베이스의 100시간 분량의 건강한 음성 녹음과 해당 글자 표기를 MFA(Montreal Forced Aligner)를 통해 음소 수준으로 정렬 및 표기했습니다.(MFA는 음소로 분류해주는 머신러닝 모델입니다.) 분할된 음소는 NC, OC, NV, OV 4가지 클래스로 그룹화 하였습니다.

DNN에 대한 입력 음성은 16kHz 샘플링 속도로 샘플링되었으며 10ms 중첩이 있는 20ms 해밍 윈도우를 사용하여 단시간 처리되었습니다. 모델은 각 20ms 프레임에서 계산된 13차원 MFCC(멜 주파수 켑스트럼 계수)와 이들의 속도(Δ) 및 가속도(ΔΔ) 계수를 포함한 39차원의 특징 벡터를 입력으로 사용했습니다. 이 모델은 네 가지 음소 범주를 분류하도록 훈련되었으며, 프레임의 레이블은 해당 프레임이 속한 범주를 나타냈습니다. 오류는 범주형 교차 엔트로피 손실 함수를 사용하여 계산되었고, ADAM 최적화 알고리즘을 사용하여 네트워크의 최적 매개변수를 추정했습니다. 이 네트워크는 학습률 0.001로 25세대 동안 훈련되었습니다.

비음 특징으로서의 DNN 사후확률

입력 음성 프레임에 대해 DNN은 NC, OC, NV, OV 클래스에 해당하는 4개의 사후확률을 생성합니다.

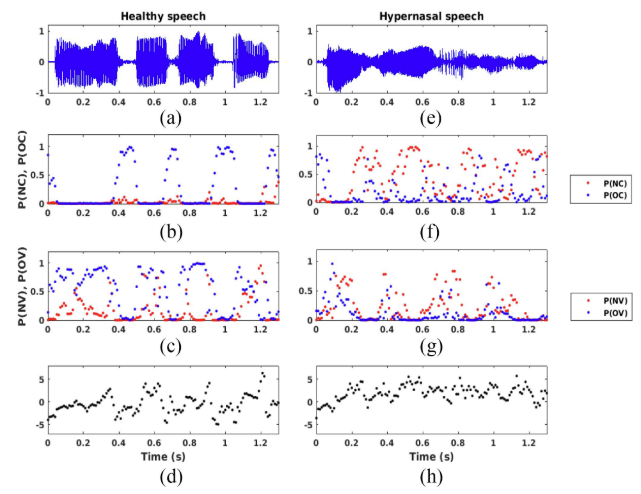Fig.5

그림 5에서와 같이 P(NC)와 P(NV)의 값이 증가하면 자음과 모음에서 각각 비음성이 있음을 의미합니다. 따라서 이러한 사후확률을 비음 특징으로 간주하고 이를 사용하여 OHM(Objective Hypernasality Mesure)를 계산합니다.

OHM 측정

OHM은 이 논문에서 제안한 과비음 측정법입니다. 지난번 논문 리뷰1 기억하시나요??

비강 자음음이 없는 문장을 발음했는데 P(NC)가 높으면?? 즉 \(P(NC|x_i)\) 가 높으면?? OHM이 커지고 과비음임을 알 수 있겠죠?? 굉장히 단순한 논리를 통해 OHM이라는 측정법을 제안했습니다.

근데 여기서 왜 비강 자음과 비강 자음의 최댓값을 이용할까요?? 논문에서 이유는 자세히 나와 있지 않아서 제가 생각해봤는데요. 일단 문장에서 비강 모음을 하나도 쓰지 않는 경우가 있습니다. 심지어 비강 모음을 콧소리를 쓰지 않고 발음을 하려면 할 수 있습니다. 그렇기 때문에 한 문장에서 비강 자음을 발음할 때는 과비음인 것 같은데. 비강 모음은 과비음이 아닌 것 같은 상황이 나올 수 있겠죠?? 이를 단순화하고 정확한 과비음 정도를 측정하기 위해 최댓값을 이용하는 것 같습니다.

마무리

여기까지가 제가 읽은 논문의 부분입니다. 이후에는 OHM의 타당성에 대해서 언급을 하고 있습니다. 자세한 인공지능 모델의 구조나 인공지능의 이론적인 언급은 없습니다.

하지만 현재 인공지능이 의료 분야에서 많이 연구되고 있고, 많은 분야중 제가 이 분야에 연구 과제에 참여할 기회가 생겨서 이 논문을 읽어보았습니다.

중간에 읽다가 MFA라는 모델이 생소하신 분들도 있으실 텐데요!! 다음에는 이 모델에 대한 논문 리뷰를 읽어볼까 합니다. 긴 글 읽어 주셔서 감사합니다😊😊